FÓRMULA COTANGENTE

La trigonometría es una rama importante de las matemáticas que se ocupa de la relación entre las longitudes de los lados y los ángulos de un triángulo rectángulo. Seno, coseno, tangente, cosecante, secante y cotangente son las seis razones o funciones trigonométricas. Donde una razón trigonométrica se representa como la razón entre los lados de un triángulo rectángulo.

sin θ = lado opuesto/hipotenusa
cos θ = lado adyacente/hipotenusa
tan θ = lado opuesto/lado adyacente
cosec θ = 1/sin θ = hipotenusa/lado opuesto
sec θ = 1/cos θ = hipotenusa/lado adyacente
cuna θ = 1/tan θ = lado adyacente/lado opuesto

Una función cotangente es una función recíproca de la función tangente dada. El valor de un ángulo cotangente en un triángulo rectángulo es la relación entre la longitud del lado adyacente al ángulo dado y la longitud del lado opuesto al ángulo dado. La función cotangente la escribimos como cot.

Triángulo ABC

Ahora, la fórmula de la cotangente para el ángulo θ es,

cuna θ = (Lado adyacente)/(Lado opuesto)

La función cotangente es positiva en el primer y tercer cuadrante y negativa en el segundo y cuarto cuadrante.

cuna (2π + θ) = cuna θ (1^callecuadrante)
cuna (π – θ) = – cuna θ (2^{Dakota del Norte}cuadrante)
cuna (π + θ) = cuna θ (3^tercerocuadrante)
cuna (2π – θ) = – cuna θ (4^thcuadrante)

La función cotangente es una función negativa ya que la cotangente de un ángulo negativo es la negativa de un ángulo cotangente positivo.

cuna (-θ) = – cuna θ

En términos de la función tangente, la función cotangente se escribe como,

cuna θ = 1/tan θ

(o)

cuna θ = tan (90° – θ) (o) tan (π/2 – θ)

La función cotangente en términos de funciones seno y coseno se puede escribir como,

cuna θ = cos θ/sen θ

Sabemos que cot θ = lado adyacente/lado opuesto

Ahora divide tanto el numerador como el denominador por la hipotenusa.
cómo revelar aplicaciones ocultas

⇒ cot θ = (lado adyacente/hipotenusa) / (lado opuesto/hipotenusa)

Sabemos que sen θ = lado opuesto/hipotenusa

cos θ = lado adyacente/hipotenusa

Por lo tanto, cot θ = cos θ/sen θ

La función cotangente en términos de función seno se puede escribir como,

cot θ = (√1 – sin ² i)/pecado i

Sabemos que cot θ = cos θ/sen θ

De las identidades pitagóricas tenemos;

porque²θ + pecado²θ = 1

⇒ cos θ = √1 – sin²i

Por lo tanto, cuna θ = $frac{sqrt{left(1-sin^{2} heta ight)}}{sin heta}$

La función cotangente en términos de función coseno se puede escribir como,

cuna θ = cos θ/(√1 -cos ² i)

Sabemos que cot θ = cos θ/sen θ

De las identidades pitagóricas tenemos;

porque²θ + pecado²θ = 1

sin θ = √1 – cos²i

Por lo tanto, cuna θ = $frac{cos heta}{sqrt{left(1-cos^{2} heta ight)}}$

La función cotangente en términos de funciones secantes y cosecantes se puede escribir como,

cuna θ = cosec θ/seg θ

Tenemos, cot θ = cos θ/sen θ

Esto se puede escribir como, cot θ = (1/sin θ) / (1/cos θ)

⇒ cot θ = cosec θ/seg θ

La función cotangente en términos de función cosecante se puede escribir como:

cuna θ = √(cosec ² – 1)

De las identidades pitagóricas, tenemos,

cosec²θ – cuna²θ = 1

⇒ cuna²θ = 1 – cosec²– 1

Por lo tanto, cot θ = √(cosec²– 1)

La función cotangente en términos de función secante se puede escribir como:

cuna θ = 1/(√seg ² yo – 1)

De las identidades pitagóricas, tenemos,

segundo²θ – tan²θ = 1

tan θ = √sec²yo – 1

Sabemos que cot θ = 1/tan θ

Por eso, cuna θ = $frac{1}{sqrt{left(1-seg^{2} heta ight)}}$

Tabla de razones trigonométricas

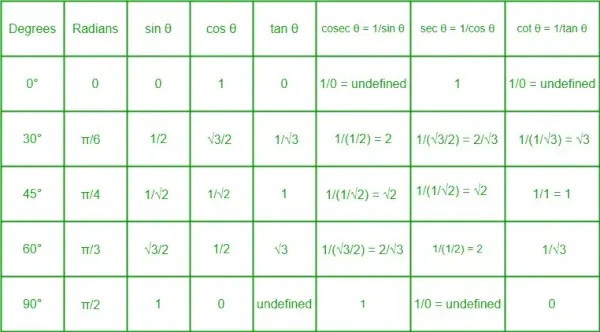
Tabla de razones trigonométricas

Ley cotangente o ley de cotangentes

La ley de la cotangente es similar a la ley del seno, pero aquí involucra semiángulos. La ley de las cotangentes describe la relación entre las longitudes de los lados del triángulo y las cotangentes de las mitades de los tres ángulos. Considere un triángulo ABC, donde a, byc son las longitudes de los lados del triángulo.

La ley de las cotangentes establece que,

$frac{cuna(frac{A}{2})}{(s-a)} = frac{cuna(frac{B}{2})}{(s-b)} = frac{cuna(frac{ C}{2})}{(s-c)} = frac{1}{r}$

Donde s es el semiperímetro del triángulo ABC y r es su radio interior de la circunferencia inscrita del triángulo.

s = (a + b + c)/2

r= $sqrt{frac{(s-a)(s-b)(s-c)}{s}}$

Problemas de muestra

Problema 1: Encuentre el valor de cot θ si tan θ = 3/4.

Solución:

Datos dados, tan θ = 3/4

Lo sabemos, cuna θ = 1/tan θ

⇒ cuna θ = 1/(3/4) = 4/3

Entonces, cuna θ = 4/3

Problema 2: Encuentre el valor de cot α, sin α = 1/3 y cos α = 2√2/3.

cual es el tamaño de mi monitor

Solución:

Dados los datos, sen α = 1/3 y cos α = 2√2/3

Lo sabemos, cuna α = cos α/sen α

⇒ cuna α = (2√2/3) / (1/3) = 2√2

Por tanto, el valor de cot α = 2√2

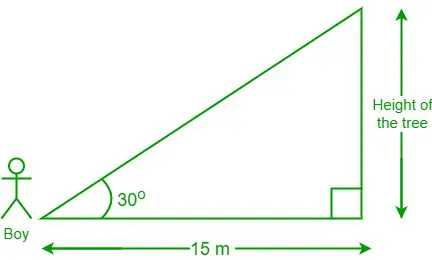
Problema 3: Un niño parado a 15 m de un árbol mira en un ángulo de 30 grados con respecto a la copa del árbol. ¿Cuál es la altura del árbol?

Solución:

Diagrama de los datos dados.

Dados los datos, la distancia entre el niño y el pie del árbol = 15 m y θ = 30°

Sea la altura del árbol 'h'

Tenemos, cuna θ = lado adyacente/lado opuesto

⇒ cuna 30° = 15/h

⇒ √3 = 15/h [ya que, cuna 30° = √3]

⇒ h = 15/√3

⇒h = 5√3m

Por tanto, la altura del árbol = 5√3 m

Problema 4: Encuentre el valor de cot x si sec x = 6/5.

Solución:

Datos dados, seg x = 6/5

Tenemos, segundo ² x – tan ² x = 1

⇒ (6/5)²– tan²x = 1

⇒ 36/25 – tan²x = 1

⇒ tan²x = 36/25 – 1

⇒ tan²x = 11/25

⇒ tan x = √(11/25) = √11/5

Lo sabemos, cot x = 1/tan x

⇒ cuna x = 1/(√11/5) = 5/√11

Por lo tanto, cot x = 5/√11

Problema 5: Encuentre el valor de cot θ si cosec θ = 25/24.

Solución:

Datos dados, cosec θ = 25/24
cómo verificar números bloqueados en Android

Lo sabemos, cuna θ = √(cosec ² – 1)

⇒ cuna θ = √(25/24)²– 1

⇒ cuna θ =√(625 – 576)/576 = √49/576

⇒ cuna θ = 7/24

Por tanto, el valor de cot θ = 7/24

Problema 6: Encuentre el valor de cot β si sen β = 5/13.

Solución:

Dados los datos, sen β = 5/13

Lo sabemos, sin ² β + porque ² b = 1

⇒ (5/13)²+ porque²b = 1

⇒ porque²β = 1 – (5/13)²= 1 – 25/169 = 144/169

⇒ porque β = √144/169 = 12/13

cuna β = cosβ/sen β

= (12/13) / (5/13)

⇒ cuna β = 12/5

Por tanto, el valor de cot β = 12/5

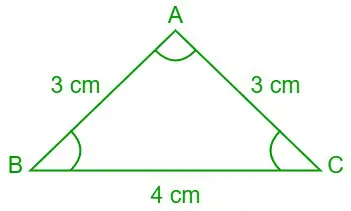
Problema 7: Usando la ley de las cotangentes, encuentre los valores de ∠A, ∠B y ∠C (en grados) si las longitudes de los tres lados del triángulo ABC son a = 4 cm, b= 3 cm y c= 3 centímetros.

Solución:

Dado, a = 4 cm, b = 3 cm y c = 3 cm

Triángulo ABC

De la ley de las cotangentes,

$frac{cuna(frac{A}{2})}{(s-a)} = frac{cuna(frac{B}{2})}{(s-b)} = frac{cuna(frac{ C}{2})}{(s-c)} = frac{1}{r}$

s = (a + b + c)/2

⇒ s = (3 + 4 + 3)/2 = 10/2 = 5

Ahora, s – a = 5 – 4 = 1

⇒ s – b = 5 – 3 = 2

⇒ s – c = 5 – 3 = 2

r= $sqrt{frac{(s-a)(s-b)(s-c)}{s}}$

⇒ r = √[(1)(2)(2)/5]

Inradio del triángulo r = 2/√5

De la ecuación de la ley de las cotangentes,

cuna (A/2)/1 = 1/(2/√5)

⇒ cuna (A/2) = √5/2 ⇒ A/2 = cuna^-1(√5/2)

⇒ (A/2) = 41,8° ⇒ ∠A = 83.6°

cuna(B/2)/2 = 1/(2/√5)

⇒ cuna(B/2)/2 = √5/2 ⇒ cuna (B/2) = √5

⇒ (B/2) = cuna^-1(√5) = 24.1° ⇒ ∠B = 48.2°

cuna (C/2)/2 = 1/(2/√5)

⇒ cuna(C/2) = √5 ⇒ (C/2) = cuna^-1(√5)

⇒ (C/2) = 24,1° ⇒ ∠C = 48.2°

Por tanto, los ángulos del triángulo ABC son ∠A = 83,6°, ∠B = 48,2° y ∠C = 48,2°.