El interés compuesto es el interés que se calcula sobre el monto de un préstamo o depósito en el que se calcula el interés para el principal y el interés anterior devengado.

La diferencia común entre interés compuesto y simple es que en interés compuesto , el interés se calcula tanto para el monto principal como para el interés ganado anteriormente, mientras que el interés simple depende únicamente del principal invertido.

Tabla de contenidos

• ¿Qué es el interés compuesto?
• Fórmula de interés compuesto
• ¿Cómo calcular el interés compuesto?
• Fórmula de interés compuesto: derivación
• Fórmula de interés compuesto semestral
• Fórmula de interés compuesto trimestral
• Fórmula de interés compuesto mensual
• Fórmula de interés compuesto diario
• Fórmula de tasa de capitalización periódica
• Regla del 72
• Interés compuesto de años consecutivos
• Fórmula de interés compuesto continuo
• Algunas otras aplicaciones del interés compuesto
• Diferencia entre interés compuesto e interés simple
• Ejemplos de interés compuesto
• Interés compuesto: preguntas de práctica

¿Qué es el interés compuesto?

El interés compuesto es el interés sobre el monto principal, así como el interés devengado sobre el monto principal. La palabra interés compuesto se compone de dos palabras. Compuesto que significa compuesto por dos o más e Interés significa dinero ganado al prestar la cantidad. Por lo tanto, el interés compuesto es el dinero que se gana al prestar y se compone de dos tipos de intereses que son:

• Intereses sobre el monto principal

• Intereses sobre los intereses devengados sobre el monto principal durante el período

Definición de interés compuesto

Interés compuesto es el interés calculado sobre el principal y los intereses devengados anteriormente. Se denota por C.I. Es muy útil para fines de inversión y pago de préstamos. También se le conoce como interés sobre interés.

Actriz Rakul Preet Singh

Interés compuesto es muy útil en los sectores bancario y financiero y también es útil en otros sectores. Algunos de sus usos son:

• Crecimiento de la población de un país.
• Valor de la inversión durante un período de tiempo.
• Para encontrar costos inflados y el valor depreciado de cualquier artículo.
• Para predecir el crecimiento de cualquier institución o país.

Interés compuesto (C.I) = Monto – Principal

Fórmula de interés compuesto

Interés compuesto se calcula, después de calcular el monto total durante un período de tiempo, en función de la tasa de interés y el principal inicial. Para un capital inicial de P, una tasa de interés anual de r, un período de tiempo t en años, una frecuencia del número de veces que el interés se capitaliza anualmente n, la fórmula para calcular CI es la siguiente:

IC = P(1 + r/100) ^norte - PAG

La fórmula anterior para calcular el interés compuesto se agrega en el formulario de imagen a continuación:

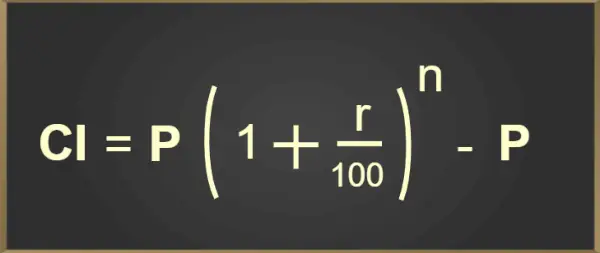
Fórmula de interés compuesto

Dónde,

• P = Principal
• r = Tasa de interés
• n = Número de veces que se capitaliza el interés por año
• t = Tiempo (en años)

Podemos escribir la fórmula del interés compuesto como:

Interés compuesto = A – P

Dónde,

• A = Cantidad total de dinero después de la capitalización
• P = Monto de capital inicial

Interés compuesto = P(1 + r/n) ^{Nuevo Testamento} -PAG

Dónde,

• P = Monto de capital inicial
• r = Tasa de interés anual
• n = Número de veces que se compone el interés
• t = Número de años

El interés compuesto se puede calcular anualmente, semestral, trimestral, mensual, diario, etc. según el requisito.

¿Cómo calcular el interés compuesto?

Interés compuesto es el interés pagado tanto sobre el principal como sobre los intereses acumulados. El interés ganado en cada intervalo se suma al principal inicial y, por lo tanto, el principal continúa aumentando.

Utilice los siguientes métodos para encontrar el interés compuesto.

Paso 1: Nota, capital, tasa y período de tiempo otorgado

Paso 2: Calcule la cantidad usando la fórmula A = P(1 + r/100) ^norte

Paso 3: Encuentre el interés compuesto usando la fórmula CI = Monto – Principal

A intervalos regulares, los intereses acumulados hasta el momento se combinan con el monto del principal existente y luego los intereses se calculado para el nuevo principal . El nuevo capital es igual a la suma del capital inicial y los intereses acumulados hasta el momento.

Interés compuesto = Interés sobre el capital + Interés sobre el interés del principal (desde el segundo año en adelante)

El interés compuesto se calcula a intervalos regulares como anualmente (anual), semestral, trimestral, mensual, etc; Es como si reinvertir los ingresos por intereses de una inversión hiciera que el dinero creciera más rápido con el tiempo. Es exactamente lo que el interés compuesto le hace al dinero. Los bancos o cualquier organización financiera calculan el monto basándose únicamente en el interés compuesto.

Fórmula de interés compuesto: derivación

La fórmula de interés compuesto es una herramienta poderosa que se utiliza en finanzas para calcular el interés ganado o pagado sobre un monto de capital inicial. que incluye tanto el principal inicial como los intereses acumulados en periodos anteriores. La fórmula del interés compuesto viene dada por:

Dónde,

• A es el valor futuro de la inversión o préstamo, incluidos los intereses.
• P es el monto principal (inversión inicial o monto del préstamo)
• r es la tasa de interés anual (como decimal)
• n es el número de veces que el interés se capitaliza por año
• Es el tiempo durante el cual se invierte o se pide prestado dinero, en años.

Fórmula de interés simple

El interés simple se calcula únicamente sobre el monto principal. Se puede representar mediante la fórmula ,

Fórmula de interés compuesto con capitalización continua

Cuando el interés se capitaliza continuamente (infinitas veces al año), la fórmula del interés compuesto se deriva utilizando la fórmula de capitalización continua:

Dónde,

• e es el número de Euler (aproximadamente 2,71828)
• P es el monto principal
• r es la tasa de interés anual
• Es tiempo en años

Fórmula de interés compuesto general

Para derivar la fórmula general del interés compuesto, consideremos el interés compuesto n veces por año.

Si P se capitaliza n veces por año a una tasa de interés anual r, el interés r se divide por n y se aplica n veces por año. Entonces, después de t años, la fórmula queda:

Dónde,

• representa la tasa de interés por período de capitalización.
• nt es el número total de períodos de capitalización a lo largo de t años.

Este La fórmula ilustra cómo el monto del capital inicial crece con el tiempo cuando el interés se compone a intervalos regulares. . A medida que n se acerca al infinito (es decir, composición continua), la fórmula converge hacia la fórmula de composición continua. .

En resumen, la fórmula del interés compuesto es el resultado de la fórmula de capitalización continua adaptada para períodos de capitalización discretos por año. Permite calcular el valor futuro de una inversión o préstamo, teniendo en cuenta el interés compuesto a intervalos regulares.

Fórmula de interés compuesto semestral

Sea el capital invertido P y la tasa de interés es R% anual, que se capitaliza semestralmente durante 't' años.

Como se capitaliza semestralmente, el capital se cambiará al final de 6 meses, y los intereses ganados hasta entonces se agregarán al capital y luego este se convertirá en el nuevo capital. Del mismo modo, se calcula el importe final.

Sabemos,

tasa = R% anual compuesto semestral

tasa = (R/2) %

el tiempo son t años sabemos que t años han 2 toneladas medio año.

Ahora,

A = P (1 + R/200) ^{2 toneladas}

IC = A – P

Fórmula de interés compuesto trimestral

Sea P el principal invertido y la tasa de interés sea R% anual, que se capitaliza trimestralmente durante t años.

Como se capitaliza trimestralmente, el capital se cambiará al final de 3 meses, y Los intereses ganados hasta ese momento se agregarán al capital y luego este se convertirá en el nuevo capital. Del mismo modo, se calcula el importe final.

sabemos,

tasa = R% anual compuesto trimestralmente

tasa = (R/4)%

shehzad poonawala

el tiempo son t años sabemos que t años han 4 toneladas cuarteles.

Ahora,

A = P(1 + R/400) ^{4 toneladas}

IC = A – P

Controlar: Fórmula de interés compuesto trimestral

Fórmula de interés compuesto mensual

Si el interés se capitaliza mensualmente, el número de veces que se capitalizará será 12 y el interés cada mes será 1/12 del interés compuesto anual. Por lo tanto, la fórmula de interés compuesto mensual se expresa como

A = P[1 + (R/1200)] ^{12 toneladas}

IC = A – P

Controlar: Fórmula de interés compuesto mensual

Fórmula de interés compuesto diario

Si el interés se capitaliza diariamente, entonces.

La nueva tasa de interés será de R/365 %

norte = 365

Por lo tanto, la fórmula del interés compuesto diario viene dada como:

A = P[1 + (R/36500)] ^365t

IC = A – P

Fórmula de tasa de capitalización periódica

El importe total, incluido el capital P y el interés compuesto CI, viene dado por:

A = P[1 + (r/n)] ^{Nuevo Testamento}

dónde,

• P = Principal
• A = Monto Final
• r = Tasa de interés anual
• n = Número de veces que el interés se capitaliza
• t = Tiempo (en años)

Así, el interés compuesto es:

IC = A – P

Regla del 72

La regla del 72 es la fórmula que se utiliza para estimar cuántos años se duplica nuestro dinero si se capitaliza anualmente. Para ejemplo , si nuestro dinero está invertido en r % Si se capitaliza anualmente, se necesitan 72/r años para que nuestro dinero se duplique.

Este cálculo también es útil para calcular el valor inflado de nuestro dinero, es decir, indica en cuántos años el valor de nuestro activo se reduce a la mitad si se deprecia anualmente.

Fórmula de la regla del 72

La siguiente fórmula se utiliza para aproximar el número de años que tardarán en duplicarse nuestra inversión.

norte = 72 / r

dónde,

• norte es el número aproximado de años en que nuestro dinero se duplicó
• r ¿Cuál es la tasa a la que nuestro dinero se capitaliza anualmente?

Ejemplo de la regla del 72

Supongamos que Kabir ha invertido 10 millones de rupias en un fondo de deuda que proporciona un rendimiento del 8%. Encuentre en cuántos años su dinero se duplica si se capitaliza anualmente.

Usando la fórmula anterior: N = 72/8 = 9 años

estructura en estructura de datos

De este modo, Se necesitan 9 años para que el dinero de Kabir se duplique.

Interés compuesto de años consecutivos

Si tenemos la misma suma y la misma tasa de interés. El CI. de un año en particular es siempre mayor que el CI del año anterior. (El IC de 3er año es mayor que el IC de 2do año). La diferencia entre CI para dos años consecutivos es el interés de un año sobre el CI del año anterior.

C.I de 3º año – C.I de 2º año = C.I de 2º año × r × 1/100

La diferencia entre los montos de dos años consecutivos es el interés de un año sobre el monto del año anterior.

Monto del 3er año – Monto del 2do año = Monto del 2do año × r × 1/100

Resultados clave

Cuando tenemos la misma suma y la misma tasa ,

C.I para el enésimo año = C.I para el (n – 1)ésimo año + Interés por un año sobre C.I para el (n – 1)ésimo año

Fórmula de interés compuesto continuo

La fórmula de capitalización continua se utiliza en finanzas para calcular el valor final de una inversión que se somete a una capitalización continua durante diferentes períodos y se agrega valor a lo largo del tiempo. La fórmula para la composición continua se da como

Valor final = Valor presente × e ^rt

dónde,

• r es la tasa de interés
• es hora

Aprende más, Fórmula de composición continua

Algunas otras aplicaciones del interés compuesto

Crecimiento: Esto se utiliza principalmente para el crecimiento si las industrias están relacionadas.

Producción después de n años = producción inicial × (1 + r/100) ^norte

Depreciación: cuando el costo de un producto se deprecia en un r% cada año, entonces su valor después de n años es

Valor presente × (1 + r/100) ^norte

Problemas de población: cuando la población de un pueblo, ciudad o aldea aumenta a una determinada tasa por año.

Población después de n años = población actual × (1 + r/100) ^norte

Diferencia entre interés compuesto e interés simple

La diferencia entre interés compuesto e interés simple se puede aprender a continuación en este artículo.

Ejemplos de interés compuesto

Algunos ejemplos de fórmulas de interés compuesto son,

Ejemplo 1: Encuentre el interés compuesto cuando el capital = 6000 rupias, la tasa = 10% anual y el tiempo = 2 años.

Solución:

Interés del primer año = (6000 × 10 × 1)/100 = 600

Monto al final del primer año = 6000 + 600 = 6600

Interés del segundo año = (6600 × 10 × 1) / 100 = 660

Monto al final del segundo año = 6600 + 660 = 7260

Interés compuesto = 7260 – 6000 = 1260

Ejemplo 2: ¿Cuál será el interés compuesto de 8000 rupias en dos años cuando la tasa de interés sea del 2% anual?

Solución:

Dado,

• Principal P = 8000
• Tasa r = 2%
• Tiempo = 2 años

por fórmula

A = P (1 + R/100) ^norte

inurl:.git/head

A = 8000 (1 + 2/100)²= 8000 (102/100)²

Un = 8323

Interés compuesto = A – P = 8323 – 8000 = Rs 323

Ejemplo 3: Hari depositó Rs. 4000 con una financiera a 2 años a un interés del 5% anual. ¿Cuál es el interés compuesto que obtiene Rohit después de 2 años?

Solución:

Dado,

• Principal P = 4000
• Tasa r = 5%
• Tiempo = 2 años

Por fórmula,

A = P (1 + R/100)^norte

Una= 4000 (1 + 5/100)²

Un= 4000 (105/100)²

Un= 4410

Interés compuesto = A – P = 4410 – 4000 = 410

Ejemplo 4: Encuentre el interés compuesto de Rs. 2000 a razón del 4 % anual durante 1,5 años. ¿Cuándo el interés se capitaliza semestralmente?

Solución:

Dado,

• Principal p = 2000
• Tasa r = 4%
• Tiempo = 1,5 (es decir, 3 medios años)

por fórmula,

A = P (1 + R/200) ²ⁿ

A = 2000 (1 + 4/200) ³

Un = 2000 (204/200) ³

Un = 2122

Interés compuesto = A – P = 2122 – 2000 = 122

Ejemplo 5: ¿Cuál es el interés compuesto de 10000 durante un año a una tasa del 20% anual, si el interés se compone trimestralmente?

Solución:

Dado,

• Principal P = 10.000 rupias
• Tasa R = 12% (12/4 = 3% por trimestre año)
• Tiempo = 1 año (1 × 4 = 4 trimestres)

Por fórmula,

A = P (1 + R/100) ^norte

A = 10000 (1 + 3/100) ⁴

Una = 10000 (103/100) ⁴

Un = 11255

Interés compuesto = A – P = 11255 – 10000 = 1255

Ejemplo 6: Encuentre el interés compuesto a una tasa del 5% anual durante 2 años sobre ese principal que en 2 años a una tasa del 5% anual dio Rs. 400 como interés simple.

Solución:

ordenar matriz en java

Dado,

• Simple Interest SI = 400
• Tasa R = 5%
• Tiempo T = 2 años

Por fórmula,

Interés simple = (P × T × R)/100

⇒ P = (SI × 100)/T × R

P = (400 × 100)/2 × 5 Tasa de interés compuesto = 5%

P = 40000/10 = 4000 rupias

Tiempo = 2 años

Por fórmula,

A = P (1 + R/100)

A = 4000 (1 + 5/100)

Un = 4410

Interés compuesto = A – P = 4410 – 4000 = 410

Ejemplo 7: Encuentre el interés compuesto de 30000 rupias al 7% de interés compuesto anualmente durante dos años.

Solución:

• Principal P = 30.000 rupias
• Tasa R = 7%
• Tiempo = 2 años

Por fórmula,

A = P (1 + R/100) ^norte

A = 30000 (1 + 7/100) ²

A = 30000 (107/100) ²

Un = 34347

Interés compuesto = A – P = 34347 – 30000 = 4347

Lecturas relacionadas:

• Interés compuesto diario
• Interés compuesto mensual
• Solución de interés compuesto clase 8
• Interés compuesto: preguntas y respuestas sobre aptitud
• Interés simple

Interés compuesto: preguntas de práctica

Varias preguntas de práctica sobre intereses compuestos son,

P1. Encuentre la cantidad que se debe pagar después de 3 años si se presta una suma de 10000 a una tasa del 4% compuesta anualmente.

P2. Encuentre el interés que debe pagarse después de 1,5 años si se presta una suma de 2500 a una tasa del 6% compuesta semestralmente.

P3. Calcule el interés compuesto de un monto de 9000 prestados a una tasa del 5% trimestral durante 15 meses.

P4. Calcule el interés compuesto de un monto de 20000 prestados a una tasa del 12% durante 3 meses con capitalización mensual

Conclusión de interés compuesto

El interés compuesto es un Potente concepto financiero que permite que las inversiones o préstamos crezcan o se acumulen con el tiempo. A diferencia de interés simple, que solo calcula el interés sobre el monto del capital inicial, interés compuesto tiene en cuenta los intereses devengados tanto sobre el principal inicial como sobre cualquier interés acumulado de períodos anteriores.

Interés compuesto: preguntas frecuentes

¿Qué significado tiene el interés compuesto?

El interés compuesto es el interés calculado sobre el capital y el interés anterior devengado durante un período de tiempo fijo.

¿Cómo calcular el interés compuesto?

Para calcular el interés compuesto, primero se calcula el monto final y luego se resta del capital para obtener el interés compuesto final. El importe se calcula mediante la fórmula,

A = P(1 + R/100) ^t

IC = A – P

¿Es el interés compuesto mejor que el interés simple para los inversores?

Sí, el interés compuesto es mucho mejor que el interés simple para los inversores.

¿Qué es la fórmula de interés compuesto si se capitaliza diariamente?

Supongamos que el principal dado es P, la tasa es R y el intervalo de tiempo es T años, entonces la fórmula del interés compuesto cuando se capitaliza diariamente es:

A = P(1 + R/365) ^{365×T}

¿Cuál es la diferencia entre CI y SI?

La diferencia básica entre CI y SI es que SI son intereses cobrados sobre el monto principal, mientras que CI son intereses cobrados sobre el monto principal, así como sobre el interés acumulado sobre el principal.