COMPRUEBE SI EXISTE UN PUNTO EN EL SECTOR CIRCULAR O NO.

Tenemos un círculo centrado en el origen (0 0). Como entrada, se nos proporciona el ángulo inicial del sector circular y el tamaño del sector circular en porcentaje.

Ejemplos:

Input : Radius = 8 StartAngle = 0 Percentage = 12 x = 3 y = 4 Output : Point (3 4) exists in the circle sector Input : Radius = 12 Startangle = 45 Percentage = 25 x = 3 y = 4 Output : Point (3 4) does not exist in the circle sector

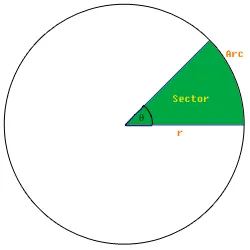Fuente: Wikibook.org

En esta imagen, el ángulo inicial es de 0 grados de radio r y supongamos que el porcentaje del área coloreada es del 12%, entonces calculamos el ángulo final como 360/porcentaje + ángulo inicial .

Para saber si un punto (x y) existe en un sector circular (centrado en el origen) o no, encontramos las coordenadas polares de ese punto y luego seguimos los siguientes pasos:

Convierta x y a coordenadas polares usando este
Ángulo = ausencia(y/x); Radio = sqrt(x * y y y y y y);
Entonces el ángulo debe estar entre el ángulo inicial y el ángulo final y el radio entre 0 y su radio.

C++

// C++ program to check if a point lies inside a circle // sector. #include   using namespace std; void checkPoint(int radius int x int y float percent  float startAngle) {  // calculate endAngle  float endAngle = 360/percent + startAngle;  // Calculate polar co-ordinates  float polarradius = sqrt(x*x+y*y);  float Angle = atan(y/x);  // Check whether polarradius is less then radius of circle  // or not and Angle is between startAngle and endAngle  // or not  if (Angle>=startAngle && Angle<=endAngle && polarradius<radius)  printf('Point (%d %d) exist in the circle sectorn' x y);  else  printf('Point (%d %d) does not exist in the circle sectorn'  x y); } // Driver code int main() {  int radius = 8 x = 3 y = 4;  float percent = 12 startAngle = 0;  checkPoint(radius x y percent startAngle);  return 0; }

Java

// Java program to check if // a point lies inside a circle // sector. class GFG { static void checkPoint(int radius int x int y float percent  float startAngle) {  // calculate endAngle  float endAngle = 360/percent + startAngle;    // Calculate polar co-ordinates  double polarradius = Math.sqrt(x*x+y*y);  double Angle = Math.atan(y/x);    // Check whether polarradius is  // less then radius of circle  // or not and Angle is between  // startAngle and endAngle  // or not  if (Angle>=startAngle && Angle<=endAngle && polarradius<radius)  System.out.print('Point'+'('+x+''+y+')'+  ' exist in the circle sectorn');  else  System.out.print('Point'+'('+x+''+y+')'+  ' exist in the circle sectorn'); } // Driver Program to test above function public static void main(String arg[]) {  int radius = 8 x = 3 y = 4;  float percent = 12 startAngle = 0;  checkPoint(radius x y percent startAngle); } } // This code is contributed // by Anant Agarwal.

Python3

# Python3 program to check if a point  # lies inside a circle sector. import math def checkPoint(radius x y percent startAngle): # calculate endAngle endAngle = 360 / percent + startAngle # Calculate polar co-ordinates polarradius = math.sqrt(x * x + y * y) Angle = math.atan(y / x) # Check whether polarradius is less # then radius of circle or not and  # Angle is between startAngle and  # endAngle or not if (Angle >= startAngle and Angle <= endAngle and polarradius < radius): print('Point (' x '' y ') ' 'exist in the circle sector') else: print('Point (' x '' y ') ' 'does not exist in the circle sector') # Driver code radius x y = 8 3 4 percent startAngle = 12 0 checkPoint(radius x y percent startAngle) # This code is contributed by # Smitha Dinesh Semwal

// C# program to check if a point lies // inside a circle sector. using System.IO; using System; class GFG {    static void checkPoint(int radius int x int y  float percent float startAngle)  {    // calculate endAngle  float endAngle = 360 / percent + startAngle;    // Calculate polar co-ordinates  float polarradius =   (float)Math.Sqrt(x * x + y * y);    float Angle = (float)Math.Atan(y / x);    // Check whether polarradius is less then   // radius of circle or not and Angle is   // between startAngle and endAngle or not  if (Angle >= startAngle && Angle <= endAngle  && polarradius < radius)  Console.Write('Point ({0} {1}) exist in '  + 'the circle sector' x y);  else  Console.Write('Point ({0} {1}) does not '  + 'exist in the circle sector' x y);  }    // Driver code  public static void Main()  {  int radius = 8 x = 3 y = 4;  float percent = 12 startAngle = 0;  checkPoint(radius x y percent startAngle);  } } // This code is contributed by Smitha Dinesh Semwal

JavaScript

<script> // Javascript program to check if // a point lies inside a circle // sector. function checkPoint(radius x y percent startAngle) {    // Calculate endAngle  let endAngle = 360 / percent + startAngle;    // Calculate polar co-ordinates  let polarradius = Math.sqrt(x * x + y * y);  let Angle = Math.atan(y / x);    // Check whether polarradius is  // less then radius of circle  // or not and Angle is between  // startAngle and endAngle  // or not  if (Angle >= startAngle &&   Angle <= endAngle &&   polarradius < radius)  document.write('Point' + '(' + x +   '' + y + ')' +  ' exist in the circle sectorn');  else  document.write('Point' + '(' + x +   '' + y + ')' +  ' exist in the circle sectorn'); }   // Driver code  let radius = 8 x = 3 y = 4; let percent = 12 startAngle = 0; checkPoint(radius x y percent startAngle); // This code is contributed by splevel62   </script>

Producción :

Point(3 4) exists in the circle sector

Complejidad del tiempo: O(1)
Espacio Auxiliar: O(1)

Crear cuestionario

TechCodeview

Compruebe si existe un punto en el sector circular o no.