La probabilidad de cartas es la probabilidad de que los eventos involucren una baraja de cartas. Como sabemos, la probabilidad es uno de los temas importantes de las matemáticas que se ocupa del cálculo de la posibilidad de cualquier evento. En palabras simples, la probabilidad de las cartas es una parte de la probabilidad en la que encontramos la probabilidad de sacar una carta de la baraja de cartas. En este artículo, aprenderemos sobre la probabilidad de las cartas con todos los detalles sobre la tabla de probabilidad de las cartas, la probabilidad de las cartas, cómo encontrar la probabilidad de las cartas y ejemplos resueltos de probabilidad de las cartas. Comencemos nuestro aprendizaje sobre el tema de la probabilidad de cartas.
¿Qué es la probabilidad?
La probabilidad es la rama de las matemáticas que estudia las posibilidades de que cualquier evento ocurra o no. Matemáticamente no es más que la relación entre el número de resultados favorables y el número total de resultados (espacio muestral) de un evento.
Algunos de los ejemplos de probabilidad de la vida real son:
- Jugar juegos de cartas, para encontrar la probabilidad de ganar o perder el juego.
- Previsión meteorológica, para predecir la lluvia.
- Resultados de las elecciones, para determinar si el candidato ganará o perderá.
- Resultados del examen, para identificar si el candidato aprobará o reprobará.
Fórmula de probabilidad
Si E es un evento con espacio muestral S y el número de resultados favorables es n(E), entonces la probabilidad del evento E, es decir, P(E), viene dada por:
P(E) = n(E) / n(S)
¿Qué es la probabilidad de tarjeta?
La probabilidad de sacar una carta o una colección de cartas de una baraja se llama probabilidad de cartas. En palabras simples, la probabilidad relacionada con los naipes se llama probabilidad de cartas. Como este es el tipo de probabilidad, siempre está entre 0 y 1. Por ejemplo, si tenemos que encontrar la probabilidad de sacar un as de la baraja de cartas, es decir, 4/52 = 1/13 [Como hay 4 ases en la baraja de 52 cartas].
Baraja de cartas en probabilidad
Deck of Cards es una colección de 52 cartas que parecen existir desde hace miles de años. Se considera que la baraja de cartas o naipes tiene su origen en India o China; la primera prueba documentada de estas cartas se encuentra en 9thChina del siglo XIX durante la dinastía Tang. Estas cartas eran similares a las cartas modernas y también estaban divididas en cuatro palos, pero el nombre y el símbolo de esos palos son diferentes, es decir, monedas, cadenas de monedas, miríadas y miríadas de decenas.
En la actualidad, estas cartas vienen en varios diseños y se dividen en cuatro palos: Espada (♠), Trébol (♣), Corazón (❤) y Diamante (◆). Para una sola carta elegida, el espacio muestral es 52, es decir, el número total de resultados para una sola carta elegida de una baraja es 52.
n(S) para baraja de cartas = 52
Tipos de cartas en una baraja
Cualquier mazo de cartas se puede clasificar de muchas formas, algunos de los parámetros sobre los cuales se pueden clasificar las cartas son:
- Basado en colores
- Basado en trajes
Entendamos esta clasificación en detalle de la siguiente manera:
Basado en colores
Según los colores, una baraja de cartas se puede clasificar en dos categorías,
- Tarjetas rojas
- Tarjetas negras
Un total de 52 cartas están divididas en partes iguales entre cartas rojas y negras, lo que significa que hay 26 cartas rojas y 26 cartas negras en la baraja.
Basado en trajes
Hay cuatro palos en la baraja de cartas que son:
- Corazones (❤)
- Diamantes (◆)
- Clubes (♣)
- Espadas (♠)
Aparte de estas, existe una clasificación más de cartas, basada en el rango de las mismas:
- As
- Tarjetas numéricas
- Tarjetas con caras
As
Ace es una de esas cartas que es la más importante o la menos importante según el juego. Esta carta A está escrita en ella y cada palo tiene una de esas cartas, es decir, cuatro cartas as.
Tarjetas numéricas
Del 2 al 10, hay 9 cartas por palo, por lo que hay un total de 36 cartas de este tipo.
Tarjetas con caras
Las tarjetas con figuras, como sugiere el nombre, contienen una figura o la cara de la figura en la tarjeta. Hay tres cartas de cada palo, es decir, jota, reina y rey. Por tanto, hay un total de 12 figuras.
Todas estas clasificaciones se pueden ver en la siguiente tabla.
| Baraja de cartas (52 cartas) | ||||
|---|---|---|---|---|
| Tarjetas de colores | Cartas Negras (26 cartas) | Tarjetas rojas (26 tarjetas) | ||
| Trajes | Espada (13 cartas) | Club (13 cartas) | Corazón (13 cartas) | Diamante (13 cartas) |
| Tarjetas con caras (12 cartas en una baraja y 3 cartas en cada palo) | K (Rey) | K (Rey) | K (Rey) | K (Rey) |
| Q (reina) | Q (reina) | Q (reina) | Q (reina) | |
| J (Jack) | J (Jack) | J (Jack) | J (Jack) | |
| Tarjetas numéricas (36 cartas en una baraja y 9 cartas en un palo) | 10 | 10 | 10 | 10 |
| 9 | 9 | 9 | 9 | |
| 8 | 8 | 8 | 8 | |
| 7 | 7 | 7 | 7 | |
| 6 | 6 | 6 | 6 | |
| 5 | 5 | 5 | 5 | |
| 4 | 4 | 4 | 4 | |
| 3 | 3 | 3 | 3 | |
| 2 | 2 | 2 | 2 | |
| Cartas as (4 cartas en baraja y 1 carta en palo) | A (as) | A (as) | A (as) | A (as) |
Tabla de baraja de cartas
El siguiente cuadro representa la clasificación de la baraja de naipes:
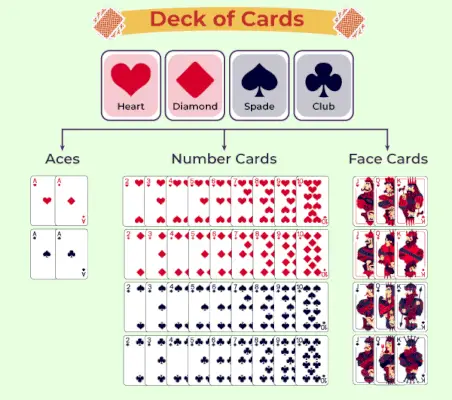
Probabilidad de naipes
Algunos de los eventos comunes en las probabilidades de cartas se analizan en la siguiente tabla:
| Evento E para robar tarjeta | Probabilidad P(E) |
|---|---|
| Un as | P(E) = 4/52 = 1/13 |
| un rey | P(E) = 4/52 = 1/13 |
| Una tarjeta numérica | P(E) = 36/52 = 9/13 |
| Una carta con cara | P(E) = 12/52 = 3/13 |
| Una carta de espadas | P(E) = 13/52 = 1/4 |
| Una tarjeta roja | P(E) = 26/52 = 1/2 poda ab |
¿Cómo encontrar la probabilidad de las cartas?
Los pasos para encontrar la probabilidad de eventos que involucran cartas son los mismos que para todas las demás probabilidades, que se dan a continuación:
Paso 1: Primero, encuentre el número de resultados favorables de la pregunta dada.
Paso 2: Luego, encuentre el número total de resultados.
Paso 3: Aplique la fórmula de probabilidad para encontrar la probabilidad de la tarjeta.
Ejemplo: ¿Cuál es la probabilidad de sacar un as de una baraja de cartas?
Respuesta:
Aquí, E es el evento de sacar una carta as.
Número total de resultados en un mazo n(S) = 52
Número de resultados favorables = n(E) = sacar una carta as del mazo = 4 (Hay 4 cartas as en 1 mazo)
P(E) = n(E) / n(S) = 4/52
P(E) = 1/13
Probabilidad de sacar un as = 1/13
Ejemplos de preguntas sobre probabilidad de cartas
Problema 1: ¿Cuál es la probabilidad de sacar las siguientes cartas de una baraja de cartas?
(i) una pala
(ii) una tarjeta negra
(iii) una tarjeta numérica
Solución:
(i) Aquí, E es el caso de sacar una carta de espadas.
Número total de resultados en un mazo n(S) = 52
Número de resultados favorables = n(E) = sacar una carta de espadas del mazo = 13 (Hay 13 cartas de cada palo en 1 mazo)
P(E) = n(E) / n(S) = 13/52
P(E) = 1/4
Probabilidad de sacar una espada = 1 / 4
(ii) Aquí, E es el caso de sacar una carta negra.
Número total de resultados en un mazo n(S) = 52
Número de resultados favorables = n(E) = sacar una carta negra del mazo = 26 (Hay 26 cartas negras en 1 mazo)
P(E) = n(E) / n(S) = 26/52
P(E) = 1/2
Probabilidad de sacar una carta negra = 1 / 2
(iii) Aquí, E es el evento de sacar una tarjeta numérica.
Número total de resultados en un mazo n(S) = 52
Número de resultados favorables = n(E) = sacar una carta numérica del mazo = 36 (Hay 36 cartas numéricas en 1 mazo)
P(E) = n(E) / n(S) = 36/52
P(E) = 9/13
Probabilidad de sacar una tarjeta numérica = 9 / 13
Problema 2: ¿Cuál es la probabilidad de sacar las siguientes cartas de una baraja de cartas?
(i) Un rey o una carta negra
(ii) Una carta roja y un as
Solución:
(i) Aquí, E es el caso de sacar un rey o una carta negra.
Número total de resultados en un mazo n(S) = 52
Número de resultados favorables = n(E) = sacar un rey o una carta negra del mazo = 26 + 2 = 28 (Hay 26 cartas negras de las cuales 2 son reyes y 2 reyes negros restantes en 1 mazo)
P(E) = n(E) / n(S) = 28/52
P(E) = 7/13
Probabilidad de sacar un rey o una carta negra = 7 / 13
(ii) Aquí, E es el evento de sacar una carta roja y un as.
Número total de resultados en un mazo n(S) = 52
Número de resultados favorables = n(E) = sacar una carta roja y un as del mazo = 2 (Hay 26 cartas rojas de las cuales 2 son cartas as)
Según la pregunta, la carta extraída debe ser roja y as. Por lo tanto, n(E) = 2
P(E) = n(E) / n(S) = 2/52
P(E) = 1/26
Probabilidad de sacar una carta roja y un as = 1/26
Problema 3: ¿Cuál es la probabilidad de sacar las siguientes cartas de una baraja de cartas?
(i) Una tarjeta que no sea del club
(ii) Una carta sin figuras
Solución:
(i) Aquí, E es el caso de sacar una carta que no pertenece al club.
Número total de resultados en un mazo n(S) = 52
Número de resultados favorables = n(E) = sacar una carta del mazo que no es de club = 39 (Hay 13 clubes en 1 mazo, sin mazo = 52 – 13 = 39)
P(E) = n(E) / n(S) = 39/52
P(E) = 3/4
Probabilidad de sacar una carta que no sea del club = 3/4
(ii) Aquí, E es el caso de sacar una carta sin figuras
Número total de resultados en un mazo n(S) = 52
Número de resultados favorables = n(E) = sacar una carta sin figuras del mazo = 40 (Hay 12 cartas con figuras en 1 mazo, sin figuras = 52 – 12 = 40)
P(E) = n(E) / n(S) = 40/52
P(E) = 10/13
Probabilidad de sacar una carta que no sea del club = 10/13
Problema 4: ¿Cuál es la probabilidad de sacar una carta que no sea roja ni figura?
Solución:
Aquí, E es el caso de sacar una carta que no es roja ni figura.
Número total de resultados en un mazo n(S) = 52
Número de resultados favorables = n(E) = no sacar ni una carta roja ni una figura del mazo.
Total de tarjetas rojas = 26
Hay un total de 12 cartas con figuras en una baraja, pero ya se han eliminado 6 cartas con figuras rojas. Entonces las figuras restantes = 12 – 6 = 6
norte(mi) = 26 + 6 = 32
P(E) = n(E) / n(S) = 32/ 52
P(E) = 8/13
Probabilidad de sacar una carta que no sea roja ni figura = 8 / 13
Problema 5: ¿Cuál es la probabilidad de sacar dos cartas de una baraja de cartas con reemplazo cuando la primera carta es de corazón y la segunda es de diamante?
Solución:
Probabilidad de sacar la primera carta como corazón = 13 / 52
Después de robar la primera carta, se retira la carta.
Probabilidad de sacar la segunda carta como diamante = 13 / 51
Probabilidad de sacar la primera carta como corazón y la segunda como diamante = (13/52) × (13/51)
Probabilidad de sacar la primera carta como corazón y la segunda como diamante = 13 / 204
Preguntas frecuentes sobre la probabilidad de la tarjeta
1. ¿Qué es la probabilidad de cartas?
La probabilidad de sacar una carta del mazo de cartas se llama probabilidad de cartas.
2. Enumere los tipos de palos en una baraja de cartas.
Hay cuatro tipos de palos en una baraja de cartas. Ellos son:
- Corazones
- diamantes
- Espadas
- Clubs
3. ¿Cuál es el espacio de muestra para la baraja de cartas cuando se extrae una carta de la baraja?
El espacio muestral de la baraja de cartas cuando se extrae una carta contiene 52 resultados.
4. Escribe la fórmula para encontrar la probabilidad.
La fórmula para encontrar la probabilidad viene dada por:
Probabilidad de evento = Número de eventos favorables / Número total de resultados
O
P(E) = n(E) / n(S)
5. ¿Cuántas cartas con figuras hay en una baraja de cartas?
Hay 12 figuras presentes en una baraja de cartas.
