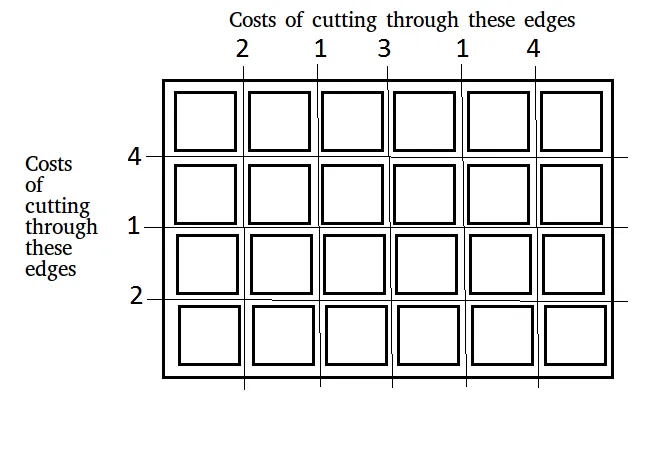
Dado un tablero de dimensiones. norte × metro que debe cortarse en n × m cuadrados. El costo de realizar un corte a lo largo de un borde horizontal o vertical se presenta en dos matrices:

• incógnita[] : Reducir costes a lo largo de los bordes verticales (longitudinalmente).
• y[] : Reducir costes a lo largo de los bordes horizontales (a lo ancho).

Encuentre el costo total mínimo requerido para cortar el tablero en cuadrados de manera óptima.

Ejemplos: 

Aporte: x[] = [2 1 3 1 4] y[] = [4 1 2] n = 4m = 6
Producción: 42
Explicación:

Inicialmente no. de segmentos horizontales = 1 y no. de segmentos verticales = 1.
La forma óptima de cortar en forma cuadrada es:
Elija 4 (de x) -> corte vertical Costo = 4 × segmentos horizontales = 4
 Ahora segmentos horizontales = 1 segmentos verticales = 2.
Elija 4 (de y) -> corte horizontal Costo = 4 × segmentos verticales = 8
 Ahora segmentos horizontales = 2 segmentos verticales = 2.
Elija 3 (de x) -> corte vertical Costo = 3 × segmentos horizontales = 6
 Ahora segmentos horizontales = 2 segmentos verticales = 3.
Elija 2 (de x) -> corte vertical Costo = 2 × segmentos horizontales = 4
 Ahora segmentos horizontales = 2 segmentos verticales = 4.
Elija 2 (de y) -> corte horizontal Costo = 2 × segmentos verticales = 8
 Ahora segmentos horizontales = 3 segmentos verticales = 4.
Elija 1 (de x) -> corte vertical Costo = 1 × segmentos horizontales = 3
Ahora segmentos horizontales = 3 segmentos verticales = 5.
Elija 1 (de x) -> corte vertical Costo = 1 × segmentos horizontales = 3
Ahora segmentos horizontales = 3 segmentos verticales = 6.
Elija 1 (de y) -> corte horizontal Costo = 1 × segmentos verticales = 6
Ahora segmentos horizontales = 4 segmentos verticales = 6.
Entonces el costo total = 4 + 8 + 6 + 4 + 8 + 3 + 3 + 6 = 42.

Aporte: x[] = [1 1 1] y[] = [1 1 1] n = 4 m = 4
Producción: 15
Explicación:
Inicialmente no. de segmentos horizontales = 1 y no. de segmentos verticales = 1.
La forma óptima de cortar en forma cuadrada es:
Elija 1 (de y) -> corte horizontal Costo = 1 × segmentos verticales = 1
Ahora segmentos horizontales = 2 segmentos verticales = 1.
Elija 1 (de y) -> corte horizontal Costo = 1 × segmentos verticales = 1
Ahora segmentos horizontales = 3 segmentos verticales = 1.
Elija 1 (de y) -> corte horizontal Costo = 1 × segmentos verticales = 1
Ahora segmentos horizontales = 4 segmentos verticales = 1.
Elija 1 (de x) -> corte vertical Costo = 1 × segmentos horizontales = 4
Ahora segmentos horizontales = 4 segmentos verticales = 2.
Elija 1 (de x) -> corte vertical Costo = 1 × segmentos horizontales = 4
Ahora segmentos horizontales = 4 segmentos verticales = 3.
Elija 1 (de x) -> corte vertical Costo = 1 × segmentos horizontales = 4
Ahora segmentos horizontales = 4 segmentos verticales = 4
Entonces el costo total = 1 + 1 + 1 + 4 + 4 + 4 = 15.

Tabla de contenido

• [Enfoque ingenuo] Pruebe todas las permutaciones: O((n+m)!×(n+m)) Tiempo y O(n+m) Espacio
• [Enfoque esperado] Uso de la técnica codiciosa: O( n (log n)+m (log m)) Tiempo y O(1) Espacio

[Enfoque ingenuo] Pruebe todas las permutaciones: O((n+m)!×(n+m)) Tiempo y O(n+m) Espacio

La idea es generar todas las permutaciones posibles de los cortes dados y luego calcular el costo de cada permutación. Finalmente devolver el coste mínimo entre ellos.

Nota: Este enfoque no es factible para entradas más grandes porque el número de permutaciones crece factorialmente como (m+n-2)!.
Para cada permutación debemos calcular el costo en O(m+n) tiempo. Por lo tanto, la complejidad del tiempo general se convierte en O((m+n−2)!×(m+n)).

[Enfoque esperado] Uso de la técnica codiciosa: O( n (log n)+m (log m)) Tiempo y O(1) Espacio

La idea es hacer primero los cortes más caros usando un enfoque codicioso . La observación es que elegir el mayor recorte de costos en cada paso reduce los costos futuros al afectar varias piezas a la vez. Clasificamos los costos de corte vertical (x) y horizontal (y) en orden descendente y luego seleccionamos iterativamente el más grande para maximizar el ahorro de costos. Los cortes restantes se procesan por separado para garantizar que todas las secciones se divida de manera óptima.

¿Qué pasa cuando hacemos un corte?

• corte horizontal → está cortando a lo ancho para que aumente el número de tiras horizontales (hCount++). Pero el costo se multiplica por vCount (el número de tiras verticales) porque el corte horizontal tiene que pasar por todos los segmentos verticales.
• corte vertical → está cortando a lo largo de la altura para que aumente el número de tiras verticales (vCount++). Pero el costo se multiplica por hCount (el número de tiras horizontales) porque el corte vertical tiene que pasar por todos los segmentos horizontales.

Pasos para resolver el problema:

• Ordene las matrices x e y en orden descendente.
• Utilice dos punteros, uno para x y otro para y, comenzando desde el valor más grande y avanzando hacia valores más pequeños.
• Mantenga hCount y vCount para realizar un seguimiento de cuántos segmentos afecta cada corte y actualizarlos en consecuencia.
• Itere mientras tanto x como y tengan cortes sin procesar, eligiendo siempre el costo mayor para minimizar los gastos generales.
• Si a x le quedan cortes, procéselos con el multiplicador hCount; Procese de manera similar los cortes en Y restantes con vCount.
• Acumule el costo total en cada paso usando la fórmula: costo reducido * número de piezas afectadas asegurando un costo mínimo.

#include   #include #include   using namespace std; int minCost(int n int m   vector<int>& x vector<int>& y) {    // Sort the cutting costs in ascending order  sort(x.begin() x.end());  sort(y.begin() y.end());   int hCount = 1 vCount = 1;   int i = x.size() - 1 j = y.size() - 1;   int totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;   vCount++;  i--;  }   else {  totalCost += y[j] * vCount;   hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost; } int main() {    int n = 4 m = 6;  vector<int> x = {2 1 3 1 4};  vector<int> y = {4 1 2};  cout << minCost(n m x y) << endl;  return 0; } 

import java.util.Arrays; class GfG {    static int minCost(int n int m   int[] x int[] y) {    // Sort the cutting costs in ascending order  Arrays.sort(x);  Arrays.sort(y);   int hCount = 1 vCount = 1;   int i = x.length - 1 j = y.length - 1;   int totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;   vCount++;  i--;  }   else {  totalCost += y[j] * vCount;   hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost;  }  public static void main(String[] args) {    int n = 4m = 6;  int[] x = {2 1 3 1 4};  int[] y = {4 1 2};  System.out.println(minCost(n m x y));  } } 

def minCost(nm x y): # Sort the cutting costs in ascending order x.sort() y.sort() hCount vCount = 1 1 i j = len(x) - 1 len(y) - 1 totalCost = 0 while i >= 0 and j >= 0: # Choose the larger cost cut to  # minimize future costs if x[i] >= y[j]: totalCost += x[i] * hCount vCount += 1 i -= 1 else: totalCost += y[j] * vCount hCount += 1 j -= 1 # Process remaining vertical cuts while i >= 0: totalCost += x[i] * hCount vCount += 1 i -= 1 # Process remaining horizontal cuts while j >= 0: totalCost += y[j] * vCount hCount += 1 j -= 1 return totalCost if __name__ == '__main__': nm = 4 6 x = [2 1 3 1 4] y = [4 1 2] print(minCost(nmx y)) 

using System; class GfG {  public static int minCost(int n int m   int[] x int[] y) {    // Sort the cutting costs in ascending order  Array.Sort(x);  Array.Sort(y);  int hCount = 1 vCount = 1;  int i = x.Length - 1 j = y.Length - 1;  int totalCost = 0;  // Process the cuts in greedy manner  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  else {  totalCost += y[j] * vCount;  hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost;  }    public static void Main() {    int n=4m=6;  int[] x = {2 1 3 1 4};  int[] y = {4 1 2};  Console.WriteLine(minCost(nm x y));  } } 

function minCost( nm x y) {    // Sort the cutting costs in ascending order  x.sort((a b) => a - b);  y.sort((a b) => a - b);  let hCount = 1 vCount = 1;  let i = x.length - 1 j = y.length - 1;  let totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;  vCount++;  i--;  }   else {  totalCost += y[j] * vCount;  hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost; } // Driver Code let n = 4m = 6; let x = [2 1 3 1 4]; let y = [4 1 2]; console.log(minCost(nm x y)); 

42