Clasificación de cubos es una técnica de clasificación que implica dividir elementos en varios grupos o cubos. Estos cubos se forman distribuyendo uniformemente los elementos. Una vez que los elementos se dividen en depósitos, se pueden ordenar utilizando cualquier otro algoritmo de clasificación. Finalmente, los elementos ordenados se reúnen de forma ordenada.
Algoritmo de clasificación de cubos:
Crear norte depósitos vacíos (o listas) y haga lo siguiente para cada elemento de la matriz arr[i].
- Insertar arr[i] en el depósito[n*array[i]]
- Ordene depósitos individuales mediante ordenación por inserción.
- Concatene todos los depósitos ordenados.
¿Cómo funciona la clasificación de cubos?
Para aplicar la clasificación por depósitos en la matriz de entrada [0.78, 0.17, 0.39, 0.26, 0.72, 0.94, 0.21, 0.12, 0.23, 0.68] , seguimos estos pasos:
Paso 1: Cree una matriz de tamaño 10, donde cada ranura represente un depósito.

Creando cubos para ordenar
Paso 2: Inserte elementos en los depósitos de la matriz de entrada según su rango.
Insertar elementos en los cubos:
matriz.de java
- Tome cada elemento de la matriz de entrada.
- Multiplique el elemento por el tamaño de la matriz del depósito (10 en este caso). Por ejemplo, para el elemento 0,23, obtenemos 0,23 * 10 = 2,3.
- Convierta el resultado a un número entero, lo que nos da el índice del depósito. En este caso, 2,3 se convierte al número entero 2.
- Inserte el elemento en el depósito correspondiente al índice calculado.
- Repita estos pasos para todos los elementos de la matriz de entrada.
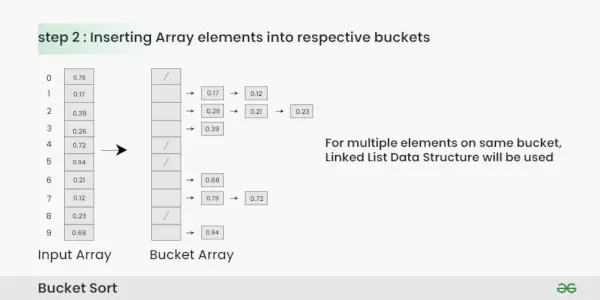
Insertar elementos de matriz en los respectivos depósitos
Paso 3: Ordena los elementos dentro de cada cubo. En este ejemplo, utilizamos la clasificación rápida (o cualquier algoritmo de clasificación estable) para ordenar los elementos dentro de cada depósito.
Ordenar los elementos dentro de cada depósito:
- Aplique un algoritmo de clasificación estable (por ejemplo, Bubble Sort, Merge Sort) para ordenar los elementos dentro de cada depósito.
- Los elementos dentro de cada depósito ahora están ordenados.
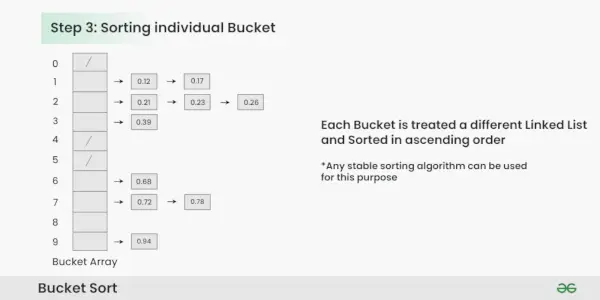
Clasificación de cubos individuales
Etapa 4: Reúna los elementos de cada cubo y vuelva a colocarlos en la matriz original.
Reuniendo elementos de cada cubo:
- Repita cada depósito en orden.
- Inserte cada elemento individual del depósito en la matriz original.
- Una vez que se copia un elemento, se elimina del depósito.
- Repita este proceso para todos los depósitos hasta que se hayan reunido todos los elementos.
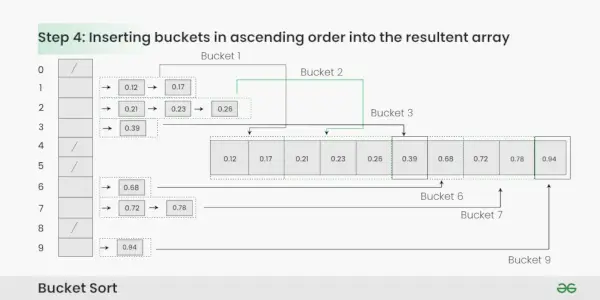
Insertar depósitos en orden ascendente en la matriz resultante
Paso 5: La matriz original ahora contiene los elementos ordenados.
La matriz ordenada final que utiliza la clasificación por cubos para la entrada dada es [0,12, 0,17, 0,21, 0,23, 0,26, 0,39, 0,68, 0,72, 0,78, 0,94].

Devolver la matriz ordenada
Implementación del algoritmo de clasificación de depósitos:
A continuación se muestra la implementación de Bucket Sort:
entero a cadenaC++
#include #include using namespace std; // Insertion sort function to sort individual buckets void insertionSort(vector& balde) { para (int i = 1; i< bucket.size(); ++i) { float key = bucket[i]; int j = i - 1; while (j>= 0 && depósito[j]> clave) { depósito[j + 1] = depósito[j]; j--; } cubo[j + 1] = clave; } } // Función para ordenar arr[] de tamaño n usando cubo sort void bucketSort(float arr[], int n) { // 1) Crear n vector de cubos vacíosb[norte]; // 2) Colocar elementos de la matriz en diferentes depósitos para (int i = 0; i< n; i++) { int bi = n * arr[i]; b[bi].push_back(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { insertionSort(b[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < b[i].size(); j++) { arr[index++] = b[i][j]; } } } // Driver program to test above function int main() { float arr[] = {0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434}; int n = sizeof(arr) / sizeof(arr[0]); bucketSort(arr, n); cout << 'Sorted array is
'; for (int i = 0; i < n; i++) { cout << arr[i] << ' '; } return 0; }>
Java import java.util.ArrayList; import java.util.List; public class Main { // Insertion sort function to sort individual buckets public static void insertionSort(Listcubo) { para (int i = 1; i< bucket.size(); ++i) { float key = bucket.get(i); int j = i - 1; while (j>= 0 && cubo.get(j)> clave) { cubo.set(j + 1, cubo.get(j)); j--; } cubo.set(j + 1, clave); } } // Función para ordenar arr[] de tamaño n usando bucket sort public static void bucketSort(float[] arr) { int n = arr.length; // 1) Crear n lista de depósitos vacíos[] depósitos = nueva ArrayList[n]; para (int i = 0; i< n; i++) { buckets[i] = new ArrayList(); } // 2) Put array elements in different buckets for (int i = 0; i < n; i++) { int bi = (int) (n * arr[i]); buckets[bi].add(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { insertionSort(buckets[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < buckets[i].size(); j++) { arr[index++] = buckets[i].get(j); } } } // Driver program to test above function public static void main(String[] args) { float[] arr = {0.897f, 0.565f, 0.656f, 0.1234f, 0.665f, 0.3434f}; bucketSort(arr); System.out.println('Sorted array is:'); for (float num : arr) { System.out.print(num + ' '); } } }> Pitón def insertion_sort(bucket): for i in range(1, len(bucket)): key = bucket[i] j = i - 1 while j>= 0 y depósito[j]> clave: depósito[j + 1] = depósito[j] j -= 1 depósito[j + 1] = clave def cubo_sort(arr): n = len(arr) depósitos = [[] for _ in range(n)] # Colocar elementos de matriz en diferentes depósitos para num in arr: bi = int(n * num) buckets[bi].append(num) # Ordenar depósitos individuales mediante ordenación por inserción para depósitos en depósitos: insertion_sort (depósito) # Concatenar todos los depósitos en arr[] index = 0 para depósito en depósitos: para num en depósito: arr[index] = num index += 1 arr = [0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434] bucket_sort (arr) print('La matriz ordenada es:') print(' '.join(map(str, arr)))> C# using System; using System.Collections.Generic; class Program { // Insertion sort function to sort individual buckets static void InsertionSort(Listcubo) { para (int i = 1; i< bucket.Count; ++i) { float key = bucket[i]; int j = i - 1; while (j>= 0 && depósito[j]> clave) { depósito[j + 1] = depósito[j]; j--; } cubo[j + 1] = clave; } } // Función para ordenar arr[] de tamaño n usando bucket sort static void BucketSort(float[] arr) { int n = arr.Length; // 1) Crear n lista de depósitos vacíos[] depósitos = nueva lista[norte]; para (int i = 0; i< n; i++) { buckets[i] = new List(); } // 2) Colocar elementos de la matriz en diferentes depósitos para (int i = 0; i< n; i++) { int bi = (int)(n * arr[i]); buckets[bi].Add(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { InsertionSort(buckets[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < buckets[i].Count; j++) { arr[index++] = buckets[i][j]; } } } // Driver program to test above function static void Main(string[] args) { float[] arr = { 0.897f, 0.565f, 0.656f, 0.1234f, 0.665f, 0.3434f }; BucketSort(arr); Console.WriteLine('Sorted array is:'); foreach (float num in arr) { Console.Write(num + ' '); } } }> javascript function insertionSort(bucket) { for (let i = 1; i < bucket.length; ++i) { let key = bucket[i]; let j = i - 1; while (j>= 0 && depósito[j]> clave) { depósito[j + 1] = depósito[j]; j--; } cubo[j + 1] = clave; } } función bucketSort(arr) { let n = arr.length; let cubos = Array.from({longitud: n}, () => []); // Coloca los elementos de la matriz en diferentes depósitos para (let i = 0; i< n; i++) { let bi = Math.floor(n * arr[i]); buckets[bi].push(arr[i]); } // Sort individual buckets using insertion sort for (let i = 0; i < n; i++) { insertionSort(buckets[i]); } // Concatenate all buckets into arr[] let index = 0; for (let i = 0; i < n; i++) { for (let j = 0; j < buckets[i].length; j++) { arr[index++] = buckets[i][j]; } } } let arr = [0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434]; bucketSort(arr); console.log('Sorted array is:'); console.log(arr.join(' '));> Producción
Sorted array is 0.1234 0.3434 0.565 0.656 0.665 0.897>
Análisis de complejidad del algoritmo de clasificación de depósitos:
Complejidad del tiempo: En2),
- Si asumimos que la inserción en un depósito toma O(1) tiempo, entonces los pasos 1 y 2 del algoritmo anterior claramente toman O(n) tiempo.
- El O(1) es fácilmente posible si usamos una lista vinculada para representar un depósito.
- El paso 4 también lleva O(n) tiempo ya que habrá n elementos en todos los depósitos.
- El paso principal a analizar es el paso 3. Este paso también toma O(n) tiempo en promedio si todos los números están distribuidos uniformemente.
Espacio Auxiliar: O(n+k)
