Un árbol binario está equilibrado si la altura del árbol es O(Log n) donde n es el número de nodos. Por ejemplo, el árbol AVL mantiene la altura O(Log n) asegurándose de que la diferencia entre las alturas de los subárboles izquierdo y derecho sea como máximo 1. Los árboles Rojo-Negro mantienen la altura O(Log n) asegurándose de que el número de nodos negros en cada ruta de raíz a hoja es el mismo y que no hay nodos rojos adyacentes. Los árboles de búsqueda binaria equilibrada tienen un buen rendimiento, ya que proporcionan tiempo O(log n) para buscar, insertar y eliminar.
Un árbol binario equilibrado es un árbol binario que sigue las 3 condiciones:
- La altura del árbol izquierdo y derecho para cualquier nodo no difiere en más de 1.
- El subárbol izquierdo de ese nodo también está equilibrado.
- El subárbol derecho de ese nodo también está equilibrado.
Un solo nodo siempre está equilibrado. También se le conoce como árbol binario de altura equilibrada.
Ejemplo :
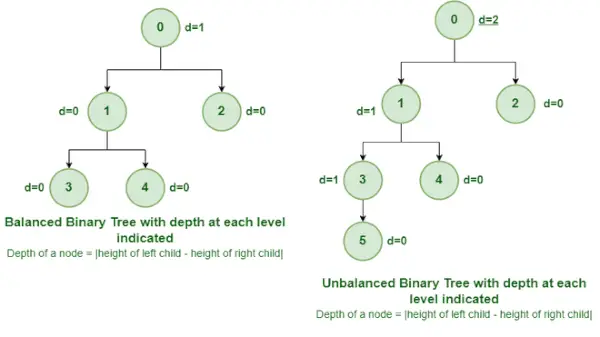
Árbol binario equilibrado y desequilibrado
Es un tipo de árbol binario en el que la diferencia entre la altura del subárbol izquierdo y derecho para cada nodo es 0 o 1. En la figura anterior, el nodo raíz que tiene un valor 0 está desequilibrado con una profundidad de 2 unidades. .
Aplicación del árbol binario equilibrado:
- Árboles AVL
- árbol negro rojo
- Árbol de búsqueda binaria equilibrado
Ventajas del árbol binario equilibrado:
- Las actualizaciones no destructivas están respaldadas por un árbol binario equilibrado con la misma efectividad asintótica.
- Las consultas de rango y la iteración en la secuencia correcta son posibles gracias al árbol binario equilibrado.
