La velocidad es simplemente la medida de qué tan rápido o lento se mueve un objeto, como qué tan rápido conduces un automóvil. Ahora bien, aquí estamos hablando de un tipo específico de velocidad. La velocidad angular es solo un tipo de velocidad, pero aquí el cuerpo debe moverse en una trayectoria circular.
Fórmula de velocidad angular
La velocidad angular se define como la tasa de cambio del desplazamiento angular, es decir, el ángulo que recorre un cuerpo a lo largo de una trayectoria circular. La velocidad angular se calcula en términos del número de rotaciones/revoluciones realizadas por un cuerpo en función del tiempo transcurrido. La velocidad angular se indica con la letra griega 'ω' conocida como Omega. La unidad SI de velocidad angular es rad/s.
La velocidad angular se calcula utilizando dos fórmulas diferentes,
- ω = θ/t ω = v/r
Derivación de fórmulas
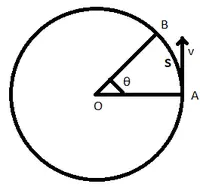
Consideremos un cuerpo que se mueve en una trayectoria circular con radio r como se muestra arriba con una velocidad lineal v. Supongamos que el cuerpo se mueve del punto A al B cubriendo una distancia s a través del arco circular y atravesando un ángulo θ en el período de tiempo t.
Camino circular recorrido por un cuerpo.
Como se sabe, la velocidad angular es la tasa de cambio de desplazamiento – Velocidad angular, ω = θ/t
Entonces la fórmula para la velocidad angular es ω = θ/t .
Otra fórmula para la velocidad angular.
A pesar de la fórmula indicada anteriormente, existe otra fórmula más utilizada para calcular la velocidad angular desde el punto de vista de los exámenes competitivos.
Como ω = θ/t ⇢ (1)
Ahora sabemos que la distancia recorrida a lo largo del arco de un círculo es igual al radio multiplicado por el ángulo recorrido. Entonces,
s = rθ
=> θ = s/r ⇢ (2)
teclas modificadorasDe (1) y (2),
ω = s/(rt) ⇢ (3)
También desde la comprensión general de las velocidades lineales,
v = s/t ⇢ (4)
De (3) y (4),
ω = v/r
Problemas de muestra
Pregunta 1: Considere un cuerpo que se mueve a lo largo de una trayectoria circular de 5 m de radio. Cubre media revolución en 5s. Calcule su velocidad angular.
Solución:
En media revolución, el ángulo que recorre es de 180 grados. En radianes, es igual a π radianes.
ω = θ/t
=> ω = π/5 = 0,628 rad/s
Pregunta 2: La rueda de un automóvil de 2 m de radio gira con una velocidad lineal de 10 m/s. Calcula su velocidad angular.
Solución:
ω = v/r
ω = 10/2
= 5 rad/s
Pregunta 3: Considere un automóvil de carreras que viaja en una pista circular con una velocidad de 18 km/h y el radio de la pista es de 0,2 m. Calcula la velocidad angular del auto.
Solución:
v = 18 km/h = 5 m/s
r = 0,2m
ω = v/r
= 5/0.2
= 25 rad/s
Pregunta 4: Un automóvil se mueve a lo largo de una trayectoria circular de 2 m de radio con una velocidad angular de 2 rad/s. Calcula el ángulo en grados que recorre el coche en 2s.
Solución:
Dado, ω = 2 rad/s y t = 2s
Dado que ω = θ/t => θ = ωt
=> θ = (2 × 2) = 4 rad
En grados, θ = 4 × (180/π) = 229,18 grados
Pregunta 5: ¿Cuántas revoluciones dio un cuerpo moviéndose a lo largo de una trayectoria circular con una velocidad angular de 7π rad/s en 0,5 s?
Solución:
Dado ω = 7π rad/s y t = 0,5 s
Dado que ω = θ/t => θ = ωt
θ = (7π × 0,5) = 3,5π
En 2π rad, las revoluciones recorridas son 1
=> En 1 rad, la revolución recorrida es (1/2π)
=> En 3,5π rad, revoluciones = 3,5π/2π = 1,75 revoluciones
Entonces, el cuerpo completará 1 revolución completa y 3/4 de la siguiente revolución en un período de tiempo de 0,5 s.
Pregunta 6: ¿Cuál será la velocidad angular de un cuerpo que se mueve en una trayectoria circular de 2 m de radio que cubre 4 m de longitud de arco de 5 s?
Solución:
Dado s = 4m, r = 2m, t = 5s
Usando la fórmula s = rθ => θ = s/r
θ = 4/2 = 2 rad
Dado que ω = θ/t
objeto a jsonobject java=> ω = 2/5 = 0,4 rad/s