El ángulo entre dos vectores es el ángulo entre sus colas y este ángulo se puede encontrar fácilmente usando el producto cruzado y el producto escalar de fórmulas vectoriales. El ángulo entre dos vectores siempre está entre 0° y 180°.

En este artículo aprenderemos en detalle sobre el ángulo entre dos vectores, su definición, fórmulas y ejemplos.

objeto java

¿Qué es el ángulo entre dos vectores?

El ángulo entre dos vectores es el ángulo que se forma en la intersección de sus colas. El ángulo entre dos vectores puede ser agudo, recto u obtuso, dependiendo de la dirección de los vectores.

El ángulo entre dos vectores se encuentra usando dos fórmulas:

• Uso del producto escalar de vectores
• Uso del producto cruzado de vectores

Esto se explica en la siguiente fórmula.

Fórmulas de ángulo entre dos vectores

Ángulo entre dos vectores se encuentra fácil y más comúnmente usando el producto escalar de vectores.

Dos vectores A y B

Producto escalar de A y B está dada por,

vec{A}.vec{B} = |A| |B| cosθ.

Casos especiales

• Cuando el ángulo entre vectores es de 0 grados.

Es decir θ = 0°

⇒ |A| |B| porqueθ

⇒ |A| |B| cos0°

⇒ |A| |B| [cos0° = 1]

• Cuando el ángulo entre vectores es de 180 grados.

⇒ |A| |B| porqueθ

⇒ |A| |B| cos180°

⇒ – |A| |B| [cos180° = -1]

• Cuando el ángulo entre vectores es de 90 grados.

⇒ |A| |B| porqueθ

⇒ |A| |B| cos90°

⇒ |A| |B| × 0 [cos90° = 0]

⇒ 0

Fórmula para el ángulo entre dos vectores

El coseno del ángulo entre dos vectores es igual a la suma del producto de los constituyentes individuales de los dos vectores, dividida por el producto de la magnitud de los dos vectores.

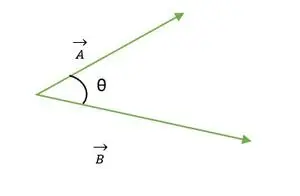
Dos vectores A y B

vec{A}.vec{B} =| Un | | B | cosθ.

cosθ=frac{vec{A}.vec{B}}B

θ= porque^-1 frac{vec{A}.vec{B}}B

En forma cartesiana,

Una = Una_Xyo + A_yj + A_Conk

segundo= segundo_Xyo + B_yj + B_Conk

porque θ =frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}

Propiedades del producto escalar

• El producto escalar es conmutativo.

vec{A}.vec{B}=vec{B}.vec{A}

• El producto escalar es distributivo

vec{A}.(vec{B}+vec{C})=(vec{A}.vec{B}+vec{A}.vec{C})

El ángulo entre dos vectores se encuentra entre 0 ≤ θ ≤ 180. Cuando las colas o cabezas de ambos vectores coinciden, se calcula el ángulo entre los vectores.

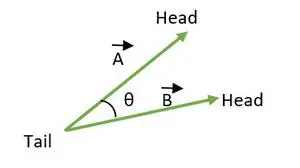
Coincidencia de cola

decodificación base64 en js

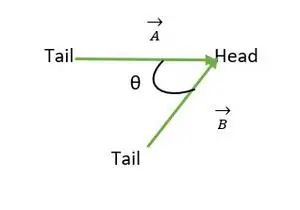
La cabeza coincide

Problemas de ejemplo Fórmula del ángulo entre dos vectores

Problema 1: Encuentra el ángulo entre vectores (Si forman un triángulo equilátero)

• vectores a y b
• Vectores de b y c
• Vectores de a y c

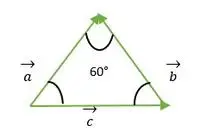
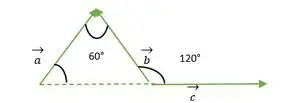
Triángulo equilátero formado por el vector a, b, c

Solución:

• vectores a y b

Para los vectores a y b, las cabezas de ambos vectores coinciden entre sí, por lo tanto, el ángulo entre los vectores a y b es el mismo que el ángulo entre dos lados de un triángulo equilátero = 60 °.

• vectores b y c:

En la figura anterior, vemos que la cabeza o la cola del vector b y c no coinciden entre sí.

Entonces, usando la propiedad: Un vector permanece sin cambios si se transmite en paralelo a sí mismo.

El vector c se desplaza paralelo a sí mismo

Ahora vemos que las colas de los vectores b y c coinciden entre sí, por lo tanto es igual que el ángulo exterior que forman con un triángulo equilátero = 120°.

• Vectores de a y c

Las colas de a y c coinciden

Para los vectores a y c, las colas de ambos vectores coinciden entre sí, por lo tanto, el ángulo entre los vectores a y c es el mismo que el ángulo entre dos lados del triángulo equilátero = 60°.

Problema 2: Encuentra ángulos entre vectores si forman un triángulo rectángulo isósceles.

• vectores a y b
• vectores b y c
• Vectores de a y c

Solución:

• vectores a y b

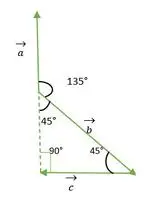
Triángulo isósceles de ángulo recto

En la figura anterior, vemos que la cabeza o la cola de los vectores a y b no coinciden entre sí. Entonces, usando la propiedad: Un vector permanece sin cambios si se transmite en paralelo a sí mismo.

un vector se desplaza paralelo a sí mismo

Ahora, las colas de los vectores a y b coinciden entre sí y forman un ángulo igual al ángulo exterior de un triángulo isósceles de ángulo recto = 135 °.

• vectores b y c

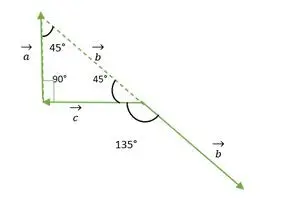
Triángulo isósceles de ángulo recto

De la figura anterior, las cabezas o colas de los vectores b y c no coinciden entre sí. Entonces, al usar la propiedad, un vector permanece sin cambios si se transmite en paralelo a sí mismo.

El vector b se desplaza paralelo a sí mismo.

Ahora, las colas de los vectores byc coinciden entre sí y forman un ángulo igual al ángulo exterior de un triángulo isósceles de ángulo recto = 135°.

• Vectores de a y c

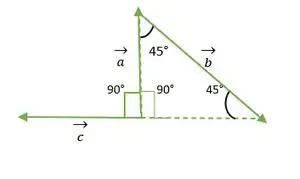
Triángulo isósceles de ángulo recto

De la figura anterior, las cabezas o colas de los vectores a y c no coinciden entre sí. Entonces, usando la propiedad: Un vector permanece sin cambios si se transmite en paralelo a sí mismo.

El vector c se mueve paralelo a sí mismo.

Ahora, las colas de los vectores a y c coinciden entre sí y forman un ángulo igual al ángulo recto del triángulo isósceles = 90°.

Problema 3: Encuentra el ángulo entre los vectores A = i + j + k y el vector B = -2i – 2j – 2k.

primavera y primavera mvc

Solución:

De la fórmula,

Una = Una_Xyo + A_yj + A_Conk

segundo= segundo_Xyo + B_yj + B_Conk

cosθ=frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}

Aquí en la pregunta dada,

A = i + j + k

B= -2i -2j -2k

Sustituyendo los valores en la fórmula.

⇒ cosθ =frac{(1.(-2)+1.(-2)+1.(-2))}{(sqrt{1^2+1^2+1^2}×sqrt{(-2)^2+(-2)^2+(-2)^2})}

⇒ cosθ =frac{(-2-2-2)}{(sqrt{1+1+1}×sqrt{4+4+4})}

⇒ cosθ =frac{-6}{(sqrt{3}×sqrt{12})}

⇒ cosθ =frac{-6}{(sqrt{36})}

⇒ cosθ = -6/6

⇒ cosθ= -1

⇒ θ = 180°

Problema 4: Encuentra el ángulo entre el vector A = 3i + 4j y B = 2i + j

Solución:

Una = Una_Xyo + A_yj + A_Conk

B = B_Xyo + B_yj + B_Conk

cosθ =frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}

Aquí dado,

A= 3i + 4j + 0k

B= 2i + j + 0k

Sustituyendo los valores en la fórmula,

⇒ cosθ =frac{(3.2+4.1+0.0)}{(sqrt{3^2+4^2+0^2}×sqrt{2^2+1^2+0^2})}

⇒ cosθ =frac{(6+4+0)}{(sqrt{9+16+0}×sqrt{4+1+0})}

mecanografiado para cada

⇒ cosθ =frac{(10)}{(sqrt{25}×sqrt{5})}

⇒ cosθ =frac{(10)}{(sqrt{125})}

⇒ θ = porque^-1(frac{(10)}{5.(sqrt{5})})

⇒ θ = porque^-1(frac{2}{(sqrt{5})})

Problema 5: Encuentra el ángulo entre el vector A = i + j y el vector B = j + k.

Solución:

De la fórmula,

Una = Una_Xyo + A_yj + A_Conk

B = B_Xyo + B_yj + B_Conk

cosθ =frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}

Aquí en la pregunta dada,

⇒ A = i + j

⇒ B = j + k

⇒ cosθ =frac{(1.0+1.1+0.1)}{(sqrt{1^2+1^2+0^2}×sqrt{0^2+1^2+1^2})}

⇒ cosθ =frac{(1)}{(sqrt{1+1+0}×sqrt{0+1+1})}

⇒ cosθ =frac{1}{(sqrt{2}×sqrt{2})}

⇒ θ = porque^-1(1/2)

⇒ θ = 60°