Una matriz 2D se puede definir como una matriz de matrices. La matriz 2D está organizada como matrices que se pueden representar como una colección de filas y columnas.
Sin embargo, las matrices 2D se crean para implementar una estructura de datos similar a una base de datos relacional. Proporciona facilidad para almacenar una gran cantidad de datos a la vez que se pueden pasar a cualquier número de funciones donde sea necesario.
Cómo declarar una matriz 2D
La sintaxis para declarar una matriz bidimensional es muy similar a la de una matriz unidimensional, como se muestra a continuación.
java reemplaza toda la cadena
int arr[max_rows][max_columns];
sin embargo, produce la estructura de datos que se parece a la siguiente.
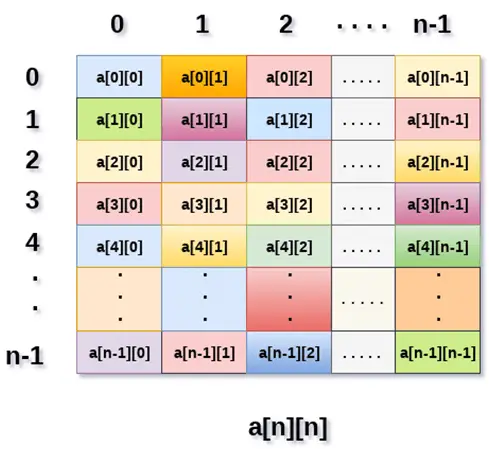
La imagen de arriba muestra la matriz bidimensional, los elementos están organizados en forma de filas y columnas. El primer elemento de la primera fila está representado por un [0] [0] donde el número que se muestra en el primer índice es el número de esa fila, mientras que el número que se muestra en el segundo índice es el número de la columna.
¿Cómo accedemos a los datos en una matriz 2D?
Debido al hecho de que se puede acceder aleatoriamente a los elementos de las matrices 2D. De manera similar a las matrices unidimensionales, podemos acceder a las celdas individuales en una matriz 2D utilizando los índices de las celdas. Hay dos índices adjuntos a una celda en particular, uno es su número de fila y el otro es su número de columna.
Sin embargo, podemos almacenar el valor almacenado en cualquier celda particular de una matriz 2D en alguna variable x usando la siguiente sintaxis.
int x = a[i][j];
donde i y j son el número de fila y columna de la celda respectivamente.
cuantas ciudades hay en estados unidos
Podemos asignar cada celda de una matriz 2D a 0 usando el siguiente código:
for ( int i=0; i<n ;i++) { for (int j="0;" j<n; j++) a[i][j]="0;" } < pre> <h2>Initializing 2D Arrays </h2> <p>We know that, when we declare and initialize one dimensional array in C programming simultaneously, we don't need to specify the size of the array. However this will not work with 2D arrays. We will have to define at least the second dimension of the array. </p> <p>The syntax to declare and initialize the 2D array is given as follows. </p> <pre> int arr[2][2] = {0,1,2,3}; </pre> <p>The number of elements that can be present in a 2D array will always be equal to ( <strong>number of rows * number of columns</strong> ). </p> <p> <strong>Example :</strong> Storing User's data into a 2D array and printing it. </p> <p> <strong>C Example : </strong> </p> <pre> #include void main () { int arr[3][3],i,j; for (i=0;i<3;i++) { for (j="0;j<3;j++)" printf('enter a[%d][%d]: ',i,j); scanf('%d',&arr[i][j]); } printf('
printing the elements ....
'); for(i="0;i<3;i++)" printf('
'); printf('%d ',arr[i][j]); < pre> <h3>Java Example</h3> <pre> import java.util.Scanner; publicclass TwoDArray { publicstaticvoid main(String[] args) { int[][] arr = newint[3][3]; Scanner sc = new Scanner(System.in); for (inti =0;i<3;i++) { for(intj="0;j<3;j++)" system.out.print('enter element'); arr[i][j]="sc.nextInt();" system.out.println(); } system.out.println('printing elements...'); for(inti="0;i<3;i++)" system.out.print(arr[i][j]+' '); < pre> <h3>C# Example </h3> <pre> using System; public class Program { public static void Main() { int[,] arr = new int[3,3]; for (int i=0;i<3;i++) { for (int j="0;j<3;j++)" console.writeline('enter element'); arr[i,j]="Convert.ToInt32(Console.ReadLine());" } console.writeline('printing elements...'); i="0;i<3;i++)" console.writeline(); console.write(arr[i,j]+' '); < pre> <h2>Mapping 2D array to 1D array </h2> <p>When it comes to map a 2 dimensional array, most of us might think that why this mapping is required. However, 2 D arrays exists from the user point of view. 2D arrays are created to implement a relational database table lookalike data structure, in computer memory, the storage technique for 2D array is similar to that of an one dimensional array. </p> <p>The size of a two dimensional array is equal to the multiplication of number of rows and the number of columns present in the array. We do need to map two dimensional array to the one dimensional array in order to store them in the memory.</p> <p>A 3 X 3 two dimensional array is shown in the following image. However, this array needs to be mapped to a one dimensional array in order to store it into the memory. </p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-2.webp" alt="DS 2D Array"> <br> <p>There are two main techniques of storing 2D array elements into memory </p> <h3>1. Row Major ordering </h3> <p>In row major ordering, all the rows of the 2D array are stored into the memory contiguously. Considering the array shown in the above image, its memory allocation according to row major order is shown as follows. </p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-3.webp" alt="DS 2D Array"> <br> <p>first, the 1<sup>st</sup> row of the array is stored into the memory completely, then the 2<sup>nd</sup> row of the array is stored into the memory completely and so on till the last row.</p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-4.webp" alt="DS 2D Array"> <br> <h3>2. Column Major ordering </h3> <p>According to the column major ordering, all the columns of the 2D array are stored into the memory contiguously. The memory allocation of the array which is shown in in the above image is given as follows.</p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-5.webp" alt="DS 2D Array"> <br> <p>first, the 1<sup>st</sup> column of the array is stored into the memory completely, then the 2<sup>nd</sup> row of the array is stored into the memory completely and so on till the last column of the array. </p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-6.webp" alt="DS 2D Array"> <br> <h2>Calculating the Address of the random element of a 2D array </h2> <p>Due to the fact that, there are two different techniques of storing the two dimensional array into the memory, there are two different formulas to calculate the address of a random element of the 2D array. </p> <h3>By Row Major Order </h3> <p>If array is declared by a[m][n] where m is the number of rows while n is the number of columns, then address of an element a[i][j] of the array stored in row major order is calculated as, </p> <pre> Address(a[i][j]) = B. A. + (i * n + j) * size </pre> <p>where, B. A. is the base address or the address of the first element of the array a[0][0] . </p> <p> <strong>Example : </strong> </p> <pre> a[10...30, 55...75], base address of the array (BA) = 0, size of an element = 4 bytes . Find the location of a[15][68]. Address(a[15][68]) = 0 + ((15 - 10) x (68 - 55 + 1) + (68 - 55)) x 4 = (5 x 14 + 13) x 4 = 83 x 4 = 332 answer </pre> <h3>By Column major order </h3> <p>If array is declared by a[m][n] where m is the number of rows while n is the number of columns, then address of an element a[i][j] of the array stored in row major order is calculated as, </p> <pre> Address(a[i][j]) = ((j*m)+i)*Size + BA </pre> <p>where BA is the base address of the array. </p> <p> <strong>Example:</strong> </p> <pre> A [-5 ... +20][20 ... 70], BA = 1020, Size of element = 8 bytes. Find the location of a[0][30]. Address [A[0][30]) = ((30-20) x 24 + 5) x 8 + 1020 = 245 x 8 + 1020 = 2980 bytes </pre> <hr></3;i++)></pre></3;i++)></pre></3;i++)></pre></n> El número de elementos que pueden estar presentes en una matriz 2D siempre será igual a ( número de filas * número de columnas ).
Ejemplo : Almacenar los datos del usuario en una matriz 2D e imprimirlos.
C Ejemplo:
#include void main () { int arr[3][3],i,j; for (i=0;i<3;i++) { for (j="0;j<3;j++)" printf(\'enter a[%d][%d]: \',i,j); scanf(\'%d\',&arr[i][j]); } printf(\'
printing the elements ....
\'); for(i="0;i<3;i++)" printf(\'
\'); printf(\'%d \',arr[i][j]); < pre> <h3>Java Example</h3> <pre> import java.util.Scanner; publicclass TwoDArray { publicstaticvoid main(String[] args) { int[][] arr = newint[3][3]; Scanner sc = new Scanner(System.in); for (inti =0;i<3;i++) { for(intj="0;j<3;j++)" system.out.print(\'enter element\'); arr[i][j]="sc.nextInt();" system.out.println(); } system.out.println(\'printing elements...\'); for(inti="0;i<3;i++)" system.out.print(arr[i][j]+\' \'); < pre> <h3>C# Example </h3> <pre> using System; public class Program { public static void Main() { int[,] arr = new int[3,3]; for (int i=0;i<3;i++) { for (int j="0;j<3;j++)" console.writeline(\'enter element\'); arr[i,j]="Convert.ToInt32(Console.ReadLine());" } console.writeline(\'printing elements...\'); i="0;i<3;i++)" console.writeline(); console.write(arr[i,j]+\' \'); < pre> <h2>Mapping 2D array to 1D array </h2> <p>When it comes to map a 2 dimensional array, most of us might think that why this mapping is required. However, 2 D arrays exists from the user point of view. 2D arrays are created to implement a relational database table lookalike data structure, in computer memory, the storage technique for 2D array is similar to that of an one dimensional array. </p> <p>The size of a two dimensional array is equal to the multiplication of number of rows and the number of columns present in the array. We do need to map two dimensional array to the one dimensional array in order to store them in the memory.</p> <p>A 3 X 3 two dimensional array is shown in the following image. However, this array needs to be mapped to a one dimensional array in order to store it into the memory. </p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-2.webp" alt="DS 2D Array"> <br> <p>There are two main techniques of storing 2D array elements into memory </p> <h3>1. Row Major ordering </h3> <p>In row major ordering, all the rows of the 2D array are stored into the memory contiguously. Considering the array shown in the above image, its memory allocation according to row major order is shown as follows. </p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-3.webp" alt="DS 2D Array"> <br> <p>first, the 1<sup>st</sup> row of the array is stored into the memory completely, then the 2<sup>nd</sup> row of the array is stored into the memory completely and so on till the last row.</p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-4.webp" alt="DS 2D Array"> <br> <h3>2. Column Major ordering </h3> <p>According to the column major ordering, all the columns of the 2D array are stored into the memory contiguously. The memory allocation of the array which is shown in in the above image is given as follows.</p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-5.webp" alt="DS 2D Array"> <br> <p>first, the 1<sup>st</sup> column of the array is stored into the memory completely, then the 2<sup>nd</sup> row of the array is stored into the memory completely and so on till the last column of the array. </p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-6.webp" alt="DS 2D Array"> <br> <h2>Calculating the Address of the random element of a 2D array </h2> <p>Due to the fact that, there are two different techniques of storing the two dimensional array into the memory, there are two different formulas to calculate the address of a random element of the 2D array. </p> <h3>By Row Major Order </h3> <p>If array is declared by a[m][n] where m is the number of rows while n is the number of columns, then address of an element a[i][j] of the array stored in row major order is calculated as, </p> <pre> Address(a[i][j]) = B. A. + (i * n + j) * size </pre> <p>where, B. A. is the base address or the address of the first element of the array a[0][0] . </p> <p> <strong>Example : </strong> </p> <pre> a[10...30, 55...75], base address of the array (BA) = 0, size of an element = 4 bytes . Find the location of a[15][68]. Address(a[15][68]) = 0 + ((15 - 10) x (68 - 55 + 1) + (68 - 55)) x 4 = (5 x 14 + 13) x 4 = 83 x 4 = 332 answer </pre> <h3>By Column major order </h3> <p>If array is declared by a[m][n] where m is the number of rows while n is the number of columns, then address of an element a[i][j] of the array stored in row major order is calculated as, </p> <pre> Address(a[i][j]) = ((j*m)+i)*Size + BA </pre> <p>where BA is the base address of the array. </p> <p> <strong>Example:</strong> </p> <pre> A [-5 ... +20][20 ... 70], BA = 1020, Size of element = 8 bytes. Find the location of a[0][30]. Address [A[0][30]) = ((30-20) x 24 + 5) x 8 + 1020 = 245 x 8 + 1020 = 2980 bytes </pre> <hr></3;i++)></pre></3;i++)></pre></3;i++)> donde, B. A. es la dirección base o la dirección del primer elemento de la matriz a[0][0] .
Ejemplo :
ordenar burbujas en java
a[10...30, 55...75], base address of the array (BA) = 0, size of an element = 4 bytes . Find the location of a[15][68]. Address(a[15][68]) = 0 + ((15 - 10) x (68 - 55 + 1) + (68 - 55)) x 4 = (5 x 14 + 13) x 4 = 83 x 4 = 332 answer
Por orden principal de columnas
Si la matriz se declara mediante a[m][n] donde m es el número de filas mientras que n es el número de columnas, entonces la dirección de un elemento a[i][j] de la matriz almacenada en el orden principal de las filas se calcula como ,
Address(a[i][j]) = ((j*m)+i)*Size + BA
donde BA es la dirección base de la matriz.
Ejemplo:
A [-5 ... +20][20 ... 70], BA = 1020, Size of element = 8 bytes. Find the location of a[0][30]. Address [A[0][30]) = ((30-20) x 24 + 5) x 8 + 1020 = 245 x 8 + 1020 = 2980 bytes
