PUNTUACIÓN Z EN ESTADÍSTICA

Puntuación Z en estadística es una medida de cuántas desviaciones estándar tiene un punto de datos de la media de una distribución. Encontremos la puntuación z en estadística. Una puntuación z de 0 indica que la puntuación del punto de datos es la misma que la puntuación media. Una puntuación z positiva indica que el punto de datos está por encima del promedio, mientras que una puntuación z negativa indica que el punto de datos está por debajo del promedio.

La fórmula para calcular una puntuación z es: z = (x – µ)/p

Dónde:

X: es el valor de la prueba
metro: es la media
en: es el valor estándar

En este artículo, vamos a discutir los siguientes conceptos:

Tabla de contenidos

¿Qué es el puntaje Z?
¿Cómo calcular la puntuación Z?
Características de la puntuación Z
Calcular valores atípicos utilizando el valor de puntuación Z
Implementación de Z-Score en Python
Aplicación de puntuación Z
Puntuaciones Z frente a desviación estándar
¿Por qué las puntuaciones Z se denominan puntuaciones estándar?

¿Qué es el puntaje Z?

La puntuación Z, también conocida como puntuación estándar, nos indica la desviación de un punto de datos de la media expresándola en términos de desviaciones estándar por encima o por debajo de la media. Nos da una idea de qué tan lejos está un punto de datos de la media. Por tanto, el Z-Score se mide en términos de desviación estándar de la media. Por ejemplo, una puntuación Z de 2 indica que el valor está a 2 desviaciones estándar de la media. Para utilizar una puntuación z, necesitamos conocer la media poblacional (μ) y también la desviación estándar poblacional (σ).

La fórmula para el puntaje Z

Se puede calcular una puntuación z utilizando la siguiente fórmula.

z = (X – µ) / p

dónde,

z = puntuación Z
X = Valor del elemento
μ = media poblacional
σ = Desviación estándar de la población

¿Cómo calcular la puntuación Z?

Se nos da la media poblacional (μ), la desviación estándar de la población (σ) y el valor observado (x) en el enunciado del problema. Al sustituirlo en la ecuación de puntuación Z, obtenemos el valor de puntuación Z. Dependiendo de si el Z-Score dado es positivo o negativo, podemos usar tabla Z positiva o tabla Z negativa disponible en línea o en la parte posterior de su libro de texto de estadística en el apéndice.

Ejemplo 1:

Usted toma el examen GATE y obtiene una puntuación de 500. La puntuación media del GATE es 390 y la desviación estándar es 45. ¿Qué tan bien obtuvo su puntuación en el examen en comparación con el examinado promedio?

Solución:

Los siguientes datos están disponibles en el enunciado de la pregunta anterior.

valor de la cadena java

Puntuación bruta/valor observado = X = 500

Puntuación media = μ = 390

Desviación estándar = σ = 45

Aplicando la fórmula del puntaje z,

z = (X – µ) / p

z = (500 – 390) / 45

z = 110/45 = 2,44

Esto significa que su puntuación z es 2.44 .

Dado que el puntaje Z es positivo 2,44, utilizaremos la tabla Z positiva.

Ahora echemos un vistazo a Mesa Z (CC-BY) para saber qué tan bien obtuvo su puntuación en comparación con los demás examinados.

Siga las instrucciones a continuación para encontrar la probabilidad de la tabla.

Aquí, puntuación z = 2,44, cual i Indica que el punto de datos está 2,44 desviaciones estándar por encima de la media.

En primer lugar, asigne los dos primeros dígitos 2,4 al eje Y.
Luego, a lo largo del eje X, mapee 0.04
Une ambos ejes. La intersección de los dos le proporcionará la probabilidad acumulada asociada con el valor de puntuación Z que está buscando.

[Esta probabilidad representa el área bajo la curva normal estándar a la izquierda del puntaje Z]

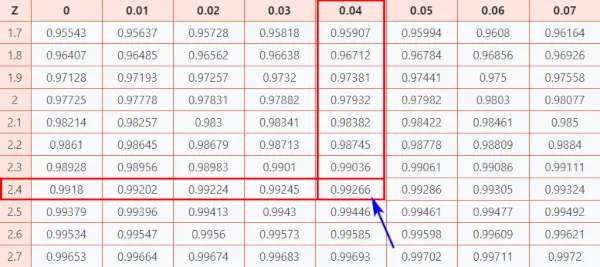
tabla de distribución normal

Como resultado, obtendrá el valor final que es 0.99266 .

Ahora, necesitamos comparar cómo se compara nuestro puntaje original de 500 en el examen GATE con el puntaje promedio del lote. Para hacer eso necesitamos convertir la probabilidad acumulada asociada con el puntaje Z en un valor porcentual.

0.99266 × 100 = 99.266%

Finalmente, puedes decir que lo has hecho mejor que casi 99% de otros examinados.

Ejemplo 2 : ¿Cuál es la probabilidad de que un estudiante obtenga una puntuación entre 350 y 400 (con una puntuación media μ de 390 y una desviación estándar σ de 45)?

Solución:

Puntuación mínima = X₁= 350

Puntuación máxima = X₂= 400

Aplicando la fórmula del puntaje z,

Con₁= (X1 – m) /p

Con₁= (350 – 390) / 45

Con₁= -40 / 45 = -0.88

Con₂= (X₂–m)/p

z2 = (400 – 390) / 45
bucle for en java

Con₂= 10 / 45 = 0.22

Como z1 es negativo, tendremos que considerar un valor negativo. Mesa Z y encuentre que la probabilidad acumulada p1, la primera probabilidad, es 0.18943 .

Con₂es positivo, por lo que utilizamos una tabla Z positiva que produce una probabilidad acumulada p₂de 0.58706 .

La probabilidad final se calcula restando p1 de p₂:

pag = pag₂- pag₁

p = 0,58706 – 0,18943 = 0,39763

La probabilidad de que un estudiante obtenga una puntuación entre 350 y 400 es 39.763% (0.39763 * 100).

Características de la puntuación Z

La magnitud del puntaje Z refleja qué tan lejos está un punto de datos de la media en términos de desviaciones estándar.
Un elemento que tiene una puntuación z inferior a 0 representa que el elemento es inferior a la media.
Las puntuaciones Z permiten comparar puntos de datos de diferentes distribuciones.
Un elemento que tiene una puntuación z mayor que 0 representa que el elemento es mayor que la media.
Un elemento que tiene una puntuación z igual a 0 representa que el elemento es igual a la media.
Un elemento que tiene una puntuación z igual a 1 representa que el elemento es 1 desviación estándar mayor que la media; una puntuación z igual a 2, 2 desviaciones estándar mayores que la media, y así sucesivamente.
Un elemento que tiene una puntuación z igual a -1 representa que el elemento es 1 desviación estándar menor que la media; una puntuación z igual a -2, 2 desviaciones estándar menores que la media, y así sucesivamente.
Si el número de elementos en un conjunto dado es grande, entonces aproximadamente el 68% de los elementos tienen una puntuación z entre -1 y 1; alrededor del 95% tiene una puntuación z entre -2 y 2; alrededor del 99% tiene una puntuación z entre -3 y 3. Esto se conoce como regla empírica y establece el porcentaje de datos dentro de ciertas desviaciones estándar de la media en una distribución normal, como se demuestra en la imagen a continuación.

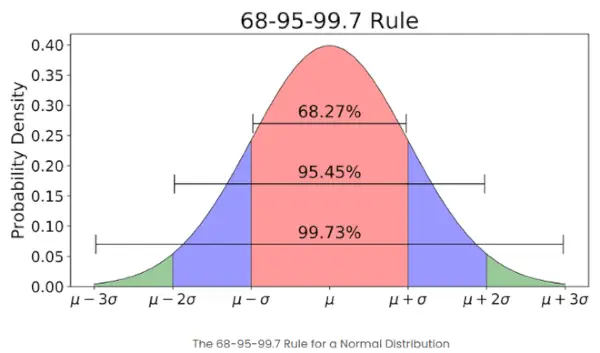
La regla empírica en la distribución normal.

Calcular valores atípicos utilizando el valor de puntuación Z

Podemos calcular valores atípicos en los datos utilizando el valor de puntuación z de los puntos de datos. Los pasos para considerar un punto de datos atípico son los siguientes:

c++ int a cadena

Al principio, recopilamos el conjunto de datos en el que queremos ver los valores atípicos.
Calcularemos la media y la desviación estándar del conjunto de datos. Estos valores se utilizarán para calcular el valor de puntuación z de cada punto de datos.
Calcularemos el valor de puntuación z para cada punto de datos. La fórmula para calcular el valor de puntuación z será la misma que
Z = frac{{X – mu}}{{sigma}}
donde X será el punto de datos, μ es la media de los datos y σ es la desviación estándar del conjunto de datos.
Determinaremos el valor límite para la puntuación z después del cual el punto de datos podría considerarse un valor atípico. Este valor de corte es un hiperparámetro que decidimos en función de nuestro proyecto.
Un punto de datos cuyo valor de puntuación z es mayor que 3 significa que el punto de datos no pertenece al punto del 99,73 % del conjunto de datos.
Cualquier punto de datos cuyo puntaje z sea mayor que nuestro valor de corte decidido se considerará un valor atípico.

Controlar: Puntuación Z para la detección de valores atípicos

Implementación de Z-Score en Python

Podemos usar Python para calcular el valor de puntuación z de los puntos de datos en el conjunto de datos. Además, usaremos la biblioteca numpy para calcular la media y la desviación estándar del conjunto de datos.

Python3

 import numpy as np def calculate_z_score(data): # Mean of the dataset mean = np.mean(data) # Standard Deviation of tha dataset std_dev = np.std(data) # Z-score of tha data points z_scores = (data - mean) / std_dev return z_scores # Example dataset dataset = [3,9, 23, 43,53, 4, 5,30, 35, 50, 70, 150, 6, 7, 8, 9, 10] z_scores = calculate_z_score(dataset) print('Z-Score :',z_scores) # Data points which lies outside 3 standard deviatioms are outliers # i.e outside range of99.73% values outliers = [data_point for data_point,  z_score in zip(dataset, z_scores) if z_score>3] print(f'
Los valores atípicos en el conjunto de datos son {valores atípicos}')>

Producción:

Puntuación Z: [-0,7574907 -0,59097335 -0,20243286 0,35262498 0,6301539 -0,72973781
-0.70198492 -0.00816262 0.13060185 0.54689523 1.10195307 3.32218443
-0.67423202 -0.64647913 -0.61872624 -0.59097335 -0.56322046]
Los valores atípicos en el conjunto de datos son [150]

Aplicación de puntuación Z

Las puntuaciones Z se utilizan a menudo para escalar características y llevar diferentes características a una escala común. Las funciones de normalización garantizan que tengan media cero y varianza unitaria, lo que puede resultar beneficioso para determinados algoritmos de aprendizaje automático, especialmente aquellos que se basan en medidas de distancia.
Las puntuaciones Z se pueden utilizar para identificar valores atípicos en un conjunto de datos. Los puntos de datos con puntuaciones Z superiores a un cierto umbral (normalmente 3 desviaciones estándar de la media) pueden considerarse valores atípicos.
Las puntuaciones Z se pueden utilizar en algoritmos de detección de anomalías para identificar instancias que se desvían significativamente del comportamiento esperado.
Las puntuaciones Z se pueden aplicar para transformar distribuciones asimétricas en distribuciones más normales.
Cuando se trabaja con modelos de regresión, se pueden analizar las puntuaciones Z de los residuos para comprobar la homocedasticidad (varianza constante de los residuos).
Las puntuaciones Z se pueden utilizar en el escalado de características observando sus desviaciones estándar de la media.

Puntuaciones Z frente a desviación estándar

Puntuación Z	Desviación Estándar
Transforme los datos sin procesar en una escala estandarizada.	Mide la cantidad de variación o dispersión en un conjunto de valores.
Facilita la comparación de valores de diferentes conjuntos de datos porque eliminan las unidades de medida originales.	La desviación estándar conserva las unidades de medida originales, lo que la hace menos adecuada para comparaciones directas entre conjuntos de datos con diferentes unidades.
Indica qué tan lejos está un punto de datos de la media en términos de desviaciones estándar, proporcionando una medida de la posición relativa del punto de datos dentro de la distribución.	Expresado en las mismas unidades que los datos originales, proporcionando una medida absoluta de qué tan dispersos están los valores alrededor de la media.

Controlar: Tabla de puntuación Z

¿Por qué las puntuaciones Z se denominan puntuaciones estándar?

Las puntuaciones Z también se conocen como puntuaciones estándar porque estandarizan el valor de una variable aleatoria. Esto significa que la lista de puntuaciones estandarizadas tiene una media de 0 y una desviación estándar de 1,0. Las puntuaciones Z también permiten comparar puntuaciones en diferentes tipos de variables. Esto se debe a que utilizan la posición relativa para equiparar puntuaciones de diferentes variables o distribuciones.

Las puntuaciones Z se utilizan con frecuencia para comparar una variable con una distribución normal estándar (con μ = 0 y σ = 1).