El Complejidad del tiempo de Combinar Ordenar es O(n iniciar sesión n) tanto en el promedio y peores casos . La complejidad espacial de Combinar ordenar es En) . 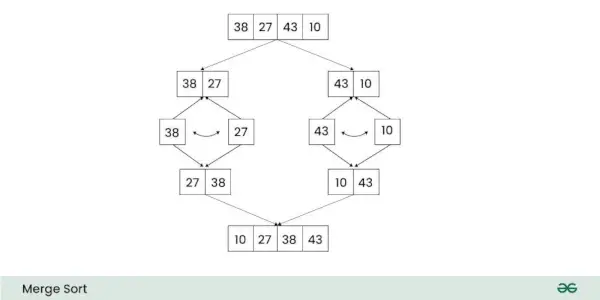
| Aspecto | Complejidad |
|---|---|
| Complejidad del tiempo | O(n iniciar sesión n) |
| Complejidad espacial | En) |
Análisis de complejidad temporal de la ordenación por combinación:
Considere las siguientes terminologías:
algoritmo knn
T(k) = tiempo necesario para ordenar k elementos
M(k) = tiempo necesario para fusionar k elementos
Entonces, se puede escribir
T(N) = 2 * T(N/2) + M(N)
= 2 * T(N/2) + constante * N
Estos N/2 elementos se dividen a su vez en dos mitades. Entonces,
T(N) = 2 * [2 * T(N/4) + constante * N/2] + constante * N
= 4 * T(N/4) + 2 * N * constante
. . .
= 2k*T(N/2k) + k * N * constante
Se puede dividir como máximo hasta que quede un elemento. Entonces, N/2k= 1. k = registro 2 norte
T(N) = N * T(1) + N * Iniciar sesión2norte * constante
= norte + norte * registro2norte
Por lo tanto la complejidad del tiempo es O(N * registro 2 NORTE) .
Entonces, en el mejor de los casos, en el peor de los casos y en el caso promedio, la complejidad del tiempo es la misma.
Análisis de complejidad espacial del ordenamiento por fusión:
Combinar ordenar tiene un complejidad espacial de En) . Esto se debe a que utiliza una matriz auxiliar de tamaño. norte para fusionar las mitades ordenadas de la matriz de entrada. La matriz auxiliar se utiliza para almacenar el resultado combinado y la matriz de entrada se sobrescribe con el resultado ordenado.
