Área de superficie de un prisma: En matemáticas, un prisma es un miembro esencial de la familia de los poliedros y se define como una forma tridimensional que tiene dos polígonos idénticos uno frente al otro que están conectados lateralmente por caras rectangulares o de paralelogramos. Los polígonos idénticos pueden ser triángulos, cuadrados, rectángulos, pentágonos o cualquier otro polígono de n lados y se denominan bases del prisma. Las otras caras de un prisma son paralelogramos o rectángulos.
pitón __dict__
En este artículo, discutiremos diferentes tipos de prismas y la fórmula del área de superficie del prisma, con ejemplos y problemas de práctica.
Tabla de contenidos
- ¿Cuál es el área de superficie del prisma?
- Diferentes tipos de prisma
- Fórmula del área de superficie del prisma
- Área de superficie de un prisma Ejemplos resueltos
- Problemas de práctica sobre el área de superficie de un prisma
¿Cuál es el área de superficie del prisma?
El área superficial de un prisma se denomina área total encerrada por todas sus caras. Para determinar el área de la superficie de un prisma, debemos calcular las áreas de cada una de sus caras y luego sumar las áreas resultantes. Un prisma tiene dos tipos de áreas de superficie, a saber, el área de superficie lateral y el área de superficie total. El área ocupada por las caras de un prisma, excluidas las dos caras paralelas (bases de un prisma), se denomina área de superficie lateral.
El área de la superficie lateral de un prisma = [perímetro de la base × altura] unidades cuadradas
Ahora bien, el área de superficie total de un prisma es la suma de las áreas de sus dos bases y su área de superficie lateral.
La fórmula general para calcular la superficie total de cualquier tipo de prisma recto es:
El área de superficie total de un prisma = [2 (área de la base) + (perímetro de la base × altura)] unidades cuadradas
Diferentes tipos de prisma
Existen diferentes tipos de prismas según la forma de la base del prisma, como
- Prismas triangulares,
- Prismas cuadrados,
- Prismas rectangulares,
- Prismas pentagonales,
- Prismas hexagonales,
- Prismas octogonales.
Prisma triangular
Un prisma con base triangular se denomina prisma triangular. Un prisma triangular consta de tres superficies rectangulares inclinadas y dos bases triangulares paralelas. Sea H la altura del prisma triangular; a, byc son las longitudes de los lados y h es la altura de las bases triangulares.
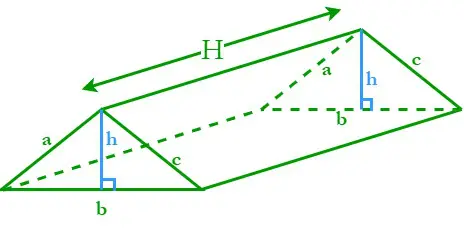
El perímetro de una base triangular (P) = Suma de sus tres lados = a + b + c
El área de una base triangular (A) = ½ × base × altura = ½ bh
Sabemos que la fórmula general para la El área de la superficie lateral de un prisma recto es L. S. A. = PH, donde P es el perímetro de la base y A es el área de la base.
Sustituyendo todos los valores en la fórmula general obtenemos ,
El área de la superficie lateral de un prisma triangular = (a + b +c)H unidades cuadradas
dónde,
a, b, c son lados de una base triangular
H es la altura del prisma triangular
Sabemos que la fórmula general para el área de superficie total de un prisma recto es T. S. A. = PH+2A, donde P es el perímetro de la base, A es el área de la base y H es la altura del prisma.
Sustituyendo todos los valores en la fórmula general obtenemos
El área de superficie total del prisma triangular = (a + b + c)H + 2 × (½ bh)
El área de superficie total del prisma triangular = (a + b + c)H + bh unidades cuadradas
dónde,
a, b, c son lados de una base triangular
H es la altura del prisma triangular
h es la altura del triángulo
Prisma rectangular
Un prisma con base rectangular se denomina prisma rectangular. Un prisma rectangular consta de cuatro superficies rectangulares y dos bases rectangulares paralelas. Sea la altura del prisma h y el largo y ancho de sus bases rectangulares sean l y w, respectivamente. .

El perímetro de una base rectangular (P) = Suma de sus cuatro lados = 2 (l + w)
El área de una base rectangular (A) = largo × ancho = l × w
Sabemos que la fórmula general para el área de la superficie lateral de un prisma recto es L. S. A. = PH, donde P es el perímetro de la base y A es el área de la base.
Sustituyendo todos los valores en la fórmula general obtenemos ,
El área de la superficie lateral de un prisma rectangular = 2h(l + w) unidades cuadradas
dónde,
l es longitud
w es ancho
su altura
Sabemos que la fórmula general para el área de superficie total de un prisma recto es T. S. A. = PH+2A, donde P es el perímetro de la base, A es el área de la base y H es la altura del prisma.
Sustituyendo todos los valores en la fórmula general obtenemos
El área de superficie total del prisma rectangular = 2h(l + w) + 2(l × w)
= 2 izquierda + 2 blanca + 2 izquierda
El área de superficie total del prisma rectangular = 2 (lh + wh + lw) unidades cuadradas
dónde,
l es longitud
w es ancho
su altura
Prisma cuadrado
Un prisma con base cuadrada se denomina prisma cuadrado. Un prisma cuadrado consta de cuatro superficies rectangulares y dos bases cuadradas paralelas. Sea la altura del prisma h y la longitud de sus bases cuadradas sea s.

El perímetro de una base cuadrada (P) = Suma de sus cuatro lados = s + s + s + s = 4s
El área de una base cuadrada (A) = (longitud del lado)2=s2
Sabemos que la fórmula general para el área de la superficie lateral de un prisma recto es L. S. A. = PH, donde P es el perímetro de la base y A es el área de la base.
Sustituyendo todos los valores en la fórmula general obtenemos,
El área de la superficie lateral de un prisma cuadrado = 4 unidades cuadradas
dónde,
s es el lado de la base cuadrada
h es la altura del prisma cuadrado
Sabemos que la fórmula general para el área de superficie total de un prisma recto es T. S. A. = PH+2A, dónde P es el perímetro de la base, A es el área de la base y H es la altura del prisma.
Sustituyendo todos los valores en la fórmula general, obtenemos
El área de superficie total del prisma cuadrado = [4sh + 2s 2 ] unidades cuadradas
dónde,
s es el lado de la base cuadrada
h es la altura del prisma cuadrado
Prisma pentagonal
Un prisma con base pentagonal se denomina prisma pentagonal. Un prisma pentagonal consta de cinco superficies rectangulares inclinadas y dos bases pentagonales paralelas. Sea h la altura del prisma pentagonal; a y b son la longitud de la apotema y las longitudes de los lados de las bases pentagonales.

El perímetro de la base de un pentágono (P) = Suma de sus cinco lados = 5b
El área de la base de un pentágono (A) = 5/2 x (longitud del apotema) x (longitud del lado) = 5ab
Sabemos que la fórmula general para el área de la superficie lateral de un prisma recto es L. S. A. = PH, donde P es el perímetro de la base y A es el área de la base.
Sustituyendo todos los valores en la fórmula general obtenemos,
El área de la superficie lateral de un prisma pentagonal = 5bh unidades cuadradas
dónde,
b es el lado de la base pentagonal
h es la altura del prisma pentagonal
Sabemos que la fórmula general para el área de superficie total de un prisma recto es T. S. A. = PH+2A, donde P es el perímetro de la base, A es el área de la base y H es la altura del prisma.
Sustituyendo todos los valores en la fórmula general obtenemos,
El área de superficie total del prisma pentagonal = [5bh + 5ab] unidades cuadradas
dónde,
b es el lado de la base pentagonal
a es la longitud de la apotema.
h es la altura del prisma pentagonal
Prisma hexagonal
Un prisma con base hexagonal se denomina prisma hexagonal. Un prisma hexagonal consta de seis superficies rectangulares inclinadas y dos bases hexagonales paralelas. Sea h la altura del prisma hexagonal; a ser las longitudes de los lados de las bases hexagonales.

El perímetro de una base hexagonal (P) = Suma de sus seis lados = 6a
El área de una base hexagonal (A) = 6 x (Área de un triángulo equilátero)
A = 6 x (√3a2/4) ⇒ A = 3√3a2/2
Sabemos que la fórmula general para el área de la superficie lateral de un prisma recto es L. S. A. = PH, donde P es el perímetro de la base y A es el área de la base.
Sustituyendo todos los valores en la fórmula general obtenemos,
El área de la superficie lateral de un prisma hexagonal = 6ah unidades cuadradas
dónde,
a es el lado de la base hexagonal
h es la altura de la base hexagonal
Sabemos que la fórmula general para el área de superficie total de un prisma recto es T. S. A. = PH+2A, donde P es el perímetro de la base, A es el área de la base y H es la altura del prisma.
Sustituyendo todos los valores en la fórmula general obtenemos
El área de superficie total del prisma hexagonal = [6ah +3√3a2] unidades cuadradas
dónde,
a es el lado de la base hexagonal
h es la altura de la base hexagonal:
Fórmula del área de superficie del prisma
La siguiente tabla proporciona la fórmula para diferentes tipos de prismas:
Forma | Base del prisma | Superficie lateral[Perímetro de la base × altura] | Superficie total[(2 × Área base) + (Perímetro base × altura)] |
|---|---|---|---|
Prisma triangular | Triángulo | (a + b +c)H unidades cuadradas | (a + b + c)H + bh unidades cuadradas |
Prisma rectangular | Rectángulo | 2h(l + w) unidades cuadradas | 2 (lh + wh + lw) unidades cuadradas |
Prisma cuadrado | Cuadrado | 4 unidades cuadradas | [4h + 2s2] unidades cuadradas |
Prisma pentagonal | Pentágono | 5bh unidades cuadradas | [5ab + 5bh] unidades cuadradas |
Prisma hexagonal | Hexágono | 6ah unidades cuadradas | [3√3a2+ 6ah] unidades cuadradas |
Área de superficie de un prisma Ejemplos resueltos
Problema 1: ¿Cuál es la altura de un prisma cuyo área de base es de 36 unidades cuadradas, su perímetro de base es de 24 unidades y su área de superficie total es de 320 unidades cuadradas?
Solución:
Datos dados,
Área base = 36 unidades cuadradas
Perímetro de la base = 24 unidades
La superficie total del prisma = 320 unidades cuadradas
Tenemos,
El área de superficie total del prisma = (2 × Área de la base) + (Perímetro de la base × altura)
⇒ 320 = (2 × 36)+ (24 × h)
⇒ 24h = 248 ⇒ h = 10,34 unidades
Por tanto, la altura del prisma dado es 10,34 unidades.
Problema 2: Encuentra el área de superficie total de un prisma cuadrado si la altura del prisma y la longitud del lado de la base cuadrada son 13 cm y 4 cm, respectivamente.
Solución:
Datos dados,
La altura del prisma cuadrado (h) = 13 cm.
La longitud del lado de la base cuadrada (a) = 4 cm.
Lo sabemos,
La superficie total de un prisma cuadrado = 2a2+ 4ah
= 2 × (4)2+ 4 × 4 × 13
= 32 + 208 = 240 centímetros2
Por lo tanto, el área de superficie total del prisma dado es 240 cm cuadrados.
Problema 3: Determine la longitud de la base de un prisma pentagonal si su área total es de 100 unidades cuadradas y su altura y longitud de apotema son de 8 unidades y 5 unidades, respectivamente.
Solución:
Datos dados,
La superficie total del prisma pentagonal = 100 unidades cuadradas
La altura del prisma (h) = 8 unidades.
Longitud del apotema (a) = 5 unidades
Lo sabemos,
La superficie total del prisma pentagonal = 5ab + 5bh
⇒ 100 = 5b (a+h)
⇒ 100/5 = b (5 + 8)
⇒ 20 = b × (13) ⇒ b = 25/16 = 1,54 unidades
Por tanto, la longitud de la base es 1,54 unidades.
Problema 4: Determine la altura del prisma rectangular y el área total de un prisma rectangular si su área de superficie lateral es 540 cm cuadrados y el largo y ancho de la base son 13 cm y 7 cm, respectivamente.
Solución:
Datos dados,
La longitud de la base rectangular (l) = 13 cm.
El ancho de la base rectangular (w) = 7 cm.
El área de la superficie lateral del prisma = 540 cm cuadrados.
Tenemos,
El área de la superficie lateral del prisma = perímetro de la base × altura
⇒ 540 = 2 (l + a) h
⇒ 2 (13 + 7) h = 540
⇒ 2 (20) h = 540 ⇒ h = 13,5 cm
Lo sabemos,
La superficie total del prisma rectangular = 2 (lw + wh + lh)
= 2 × (13 × 7 + 7 × (13.5) + 13 × (13.5))
= 2 × (91 + 94,5 + 175,5) = 722 cm2
Por lo tanto, la altura y el área de superficie total del prisma rectangular dado son 13,5 cm y 722 cm cuadrados, respectivamente.
Problema 5: Determine el área de la superficie del prisma hexagonal regular si la altura del prisma es de 12 pulgadas y la longitud del lado de la base es de 5 pulgadas.
Solución:
Datos dados,
La altura del prisma (h) = 12 pulgadas.
La longitud del lado de la base (a) = 6 pulg.
El área de superficie de un prisma hexagonal regular = 6ah + 3√3a2
= 6 × 5 × 12 + 3√3(5)2
= 360 + 75√3
= 360 + 75 × (1,732) = 489,9 pulgadas cuadradas
Por lo tanto, el área de superficie del prisma dado es 489,9 pulgadas cuadradas.
Problema 6: Calcule las áreas de superficie lateral y total de un prisma triangular cuyo perímetro de base es de 25 pulgadas, la longitud y la altura de la base del triángulo son de 9 pulgadas y 10 pulgadas, y la altura del prisma es de 14 pulgadas.
Solución:
Datos dados,
La altura del prisma (H) = 14 pulgadas
El perímetro de la base del prisma (P) = 25 pulgadas
La longitud de la base del triángulo = 9 pulgadas.
La altura del triángulo = 10 pulgadas.
Lo sabemos,
El área de la superficie lateral del prisma = perímetro de la base × altura
= 25 × 14 = 350 pulgadas cuadradas
Área de la base triangular (A) = ½ × base × altura = 1/2 × 9 × 10 = 45 pulgadas cuadradas
La superficie total del prisma triangular = 2A + PH
= 2 × 45 + 25 × 14 = 90 + 350 = 440 pulgadas cuadradas
Por lo tanto, las áreas de superficie lateral y total del prisma son 350 pulgadas cuadradas y 440 pulgadas cuadradas, respectivamente.
Problemas de práctica sobre el área de superficie de un prisma
1. Dado un prisma rectangular con dimensiones:
- Longitud = 6 cm
- Ancho = 4cm
- Altura = 5cm
Calcula la superficie total.
2. Considere un prisma triangular con dimensiones:
- Base del triángulo = 8 cm
- Altura del triángulo = 6 cm
- Longitud del prisma = 10 cm
Encuentra el área de superficie total.
3. Determina el área de superficie de un prisma pentagonal regular con:
- Longitud lateral de la base = 7 cm
- Altura del prisma = 9 cm.
4. Calcula el área de superficie de un prisma hexagonal con:
- Longitud lateral de la base hexagonal regular = 10 cm
- Altura del prisma = 12 cm.
Área de superficie de un prisma: preguntas frecuentes
¿Qué es un prisma en geometría?
Un prisma es una forma tridimensional con dos bases paralelas congruentes y caras laterales rectangulares o de paralelogramo que las conectan. Los prismas vienen en varias formas, como prismas rectangulares, prismas triangulares y prismas pentagonales, cada uno con características únicas.
¿Cómo se encuentra el área de superficie de un prisma?
Para encontrar el área de la superficie de un prisma, calcula las áreas de todas sus caras y luego resúmalas. Para un prisma rectangular, la fórmula del área de superficie es 2lw + 2lh + 2wh, donde l es la longitud, w es el ancho y h es la altura. Para otros tipos de prismas, como los triangulares o pentagonales, es posible que se necesiten fórmulas adicionales para el área de la base y el área lateral.
¿Cuáles son las propiedades de un prisma?
Los prismas tienen varias propiedades clave:
- Tienen dos bases paralelas congruentes.
- Las caras laterales son todas paralelogramos.
- La altitud (altura) es la distancia perpendicular entre las dos bases.
- Las bases son idénticas en forma y tamaño.
- La sección transversal paralela a las bases tiene siempre la misma forma y tamaño que las bases.
¿Cuáles son algunos ejemplos de prismas de la vida real?
Los prismas se pueden encontrar en diversos objetos y estructuras cotidianos. Ejemplos incluyen:
- Prismas rectangulares: Edificios, cajas de cereales, libros.
- Prismas triangulares: Tejados de casas, objetos en forma de cuña.
- Prismas pentagonales: Algunos tipos de columnas, determinadas estructuras arquitectónicas.
- Prismas hexagonales: Ciertos tipos de cristales, algunos envases.
¿Por qué es importante el área de superficie en los prismas?
El área de la superficie es crucial en los prismas ya que representa el área total de todas las superficies (caras) del prisma. Comprender el área de la superficie ayuda en diversas aplicaciones prácticas, como calcular la cantidad de material necesario para construir o cubrir un objeto con forma de prisma, determinar las tasas de transferencia de calor y optimizar el diseño del empaque.
