Una función recursiva se puede definir como una rutina que se llama a sí misma directa o indirectamente.
En otras palabras, una función recursiva es una función que resuelve un problema resolviendo instancias más pequeñas del mismo problema. Esta técnica se usa comúnmente en programación para resolver problemas que se pueden dividir en subproblemas similares más simples.
insertar marca de agua en word
Necesidad de función recursiva:
Una función recursiva es una función que resuelve un problema resolviendo instancias más pequeñas del mismo problema. Esta técnica se utiliza a menudo en programación para resolver problemas que se pueden dividir en subproblemas similares más simples.
1. Resolver tareas complejas:
Las funciones recursivas dividen problemas complejos en instancias más pequeñas del mismo problema, lo que da como resultado un código compacto y legible.
2. Divide y vencerás:
Las funciones recursivas son adecuadas para algoritmos de divide y vencerás, como la clasificación por combinación y la clasificación rápida, que dividen los problemas en subproblemas más pequeños, los resuelven de forma recursiva y fusionan las soluciones con el problema original.
3. Retroceder :
El retroceso recursivo es ideal para explorar y resolver problemas como N-Queens y Sudoku.
4. Dinámico programación:
Las funciones recursivas resuelven eficientemente problemas de programación dinámica resolviendo subproblemas y combinando sus soluciones en una solución completa.
escaneo.siguientecadena java
5. Árbol y estructuras gráficas:
Las funciones recursivas son excelentes para trabajar con estructuras de árboles y gráficos, simplificando las tareas de recorrido y reconocimiento de patrones. .
Cómo escribir una función recursiva:
Componentes de una función recursiva:
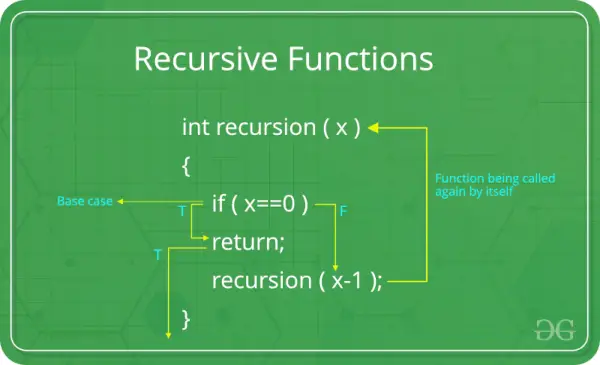
Caso base: Toda función recursiva debe tener un caso base. El caso base es el escenario más simple que no requiere mayor recursividad. Esta es una condición de terminación que impide que la función se llame a sí misma indefinidamente. Sin un caso base adecuado, una función recursiva puede conducir a una recursividad infinita.
ordenación por inserción en java
Caso recursivo: En el caso recursivo, la función se llama a sí misma con los argumentos modificados. Ésta es la esencia de la recursividad: resolver un problema mayor dividiéndolo en instancias más pequeñas del mismo problema. El caso recursivo debería acercarse al caso base con cada iteración.
Consideremos el ejemplo de factorial de numero :
En este ejemplo, el caso base es cuando norte es 0 , y la función regresa 1 . El caso recursivo se multiplica. norte con el resultado de la función llamada con parámetro norte – 1 . El proceso continúa hasta llegar al caso base.
Es esencial garantizar que la función recursiva tenga un caso base correcto y que las llamadas recursivas conduzcan al caso base; de lo contrario, el procedimiento podría ejecutarse indefinidamente, lo que provocaría un desbordamiento de la pila (excediendo la memoria disponible asignada para las llamadas a funciones).
A continuación se muestra la implementación del factorial de un número:
C++ #include using namespace std; // Recursive Function to calculate Factorial of a number int factorial(int n) { // Base case if (n == 0) { return 1; } // Recursive case return n * factorial(n - 1); } // Driver Code int main() { int n = 4; cout << 'Factorial of ' << n << ' is:' << factorial(n); return 0; }> Java import java.util.Scanner; public class Factorial { // Recursive Function to calculate the factorial of a number static int factorial(int n) { // Base case: If n is 0, the factorial is 1. if (n == 0) { return 1; } // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1). return n * factorial(n - 1); } public static void main(String[] args) { int n = 4; // Calculate and print the factorial of n. int result = factorial(n); System.out.println('Factorial of ' + n + ' is: ' + result); } }> Pitón # Recursive Function to calculate Factorial of a number def factorial(n): # Base case if n == 0: return 1 # Recursive case return n * factorial(n - 1) # Driver Code if __name__ == '__main__': n = 4 print('Factorial of', n, 'is:', factorial(n))> C# using System; class Program { // Recursive Function to calculate Factorial of a number static int Factorial(int n) { // Base case if (n == 0) { return 1; } // Recursive case return n * Factorial(n - 1); } // Driver Code static void Main() { int n = 4; Console.WriteLine('Factorial of ' + n + ' is: ' + Factorial(n)); } }> JavaScript // Function to calculate the factorial of a number using recursion function factorial(n) { // Base case: If n is 0, the factorial is 1. if (n === 0) { return 1; } // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1). return n * factorial(n - 1); } // Main function function main() { // Given number let n = 4; // Calculate the factorial of n. let result = factorial(n); // Print the result console.log('Factorial of ' + n + ' is: ' + result); } // Call the main function main();> Producción
Factorial of 4 is:24>
Complejidad del tiempo: En)
Espacio Auxiliar: En)
Linux cambiar el nombre del directorio
