- Los autómatas pushdown son una forma de implementar un CFG de la misma manera que diseñamos DFA para una gramática normal. Un DFA puede recordar una cantidad finita de información, pero una PDA puede recordar una cantidad infinita de información.
- Los autómatas pushdown son simplemente una NFA aumentada con una 'memoria de pila externa'. La adición de pila se utiliza para proporcionar una capacidad de administración de memoria de último en entrar, primero en salir a los autómatas Pushdown. Los autómatas pushdown pueden almacenar una cantidad ilimitada de información en la pila. Puede acceder a una cantidad limitada de información en la pila. Una PDA puede empujar un elemento a la parte superior de la pila y sacar un elemento de la parte superior de la pila. Para leer un elemento en la pila, los elementos superiores deben extraerse y se pierden.
- Una PDA es más poderosa que una FA. Cualquier lenguaje que pueda ser aceptable para FA también puede ser aceptable para PDA. PDA también acepta una clase de lenguaje que ni siquiera puede ser aceptado por FA. Por tanto, PDA es mucho más superior a FA.
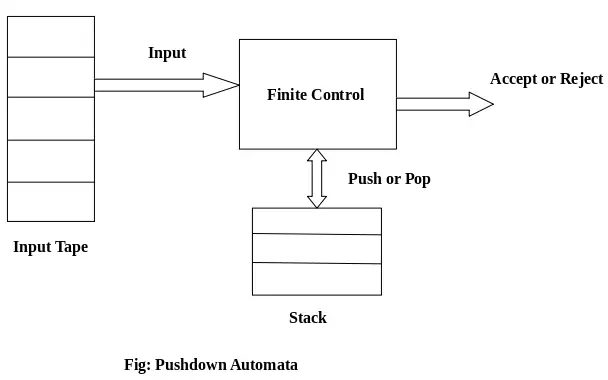
Componentes de la PDA:
Cinta de entrada: La cinta de entrada está dividida en muchas celdas o símbolos. El cabezal de entrada es de sólo lectura y sólo puede moverse de izquierda a derecha, un símbolo a la vez.
Control finito: El control finito tiene un puntero que señala el símbolo actual que se va a leer.
Pila: La pila es una estructura en la que podemos empujar y sacar los elementos por un solo extremo. Tiene un tamaño infinito. En PDA, la pila se utiliza para almacenar elementos temporalmente.
Definición formal de PDA:
La PDA se puede definir como un conjunto de 7 componentes:
P: el conjunto finito de estados
∑: el conjunto de entrada
C: un símbolo de pila que se puede empujar y sacar de la pila
q0: el estado inicial
dialecto de hibernación
CON: un símbolo de inicio que está en Γ.
F: un conjunto de estados finales
d: Función de mapeo que se utiliza para pasar del estado actual al siguiente.
Descripción instantánea (ID)
ID es una notación informal de cómo una PDA calcula una cadena de entrada y toma la decisión de aceptar o rechazar esa cadena.
Una descripción instantánea es una tripleta (q, w, α) donde:
q describe el estado actual.
En describe la entrada restante.
superíndice en ilustrador
a describe el contenido de la pila, arriba a la izquierda.
Notación de torniquete:
El signo ⊢ describe la notación del torniquete y representa un movimiento.
El signo ⊢* describe una secuencia de movimientos.
Por ejemplo,
(p, b, T) ⊢ (q, w, α)
En el ejemplo anterior, mientras se realiza una transición del estado p al q, el símbolo de entrada 'b' se consume y la parte superior de la pila 'T' se representa mediante una nueva cadena α.
Ejemplo 1:
Diseñar una PDA para aceptar un idiomanorteb2n.
Solución: En este lenguaje, n número de a deben ir seguidos de 2n número de b. Por lo tanto, aplicaremos una lógica muy simple, y es que si leemos una sola 'a', colocaremos dos a en la pila. Tan pronto como leamos 'b', por cada 'b' solo debería extraerse una 'a' de la pila.
cadena ti int
La identificación se puede construir de la siguiente manera:
δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa)
Ahora, cuando leamos b, cambiaremos el estado de q0 a q1 y comenzaremos a mostrar la 'a' correspondiente. Por eso,
δ(q0, b, a) = (q1, ε)
Por lo tanto, este proceso de extraer 'b' se repetirá a menos que se lean todos los símbolos. Tenga en cuenta que la acción de estallido ocurre sólo en el estado q1.
δ(q1, b, a) = (q1, ε)
Después de leer todas las b, todas las a correspondientes deberían aparecer. Por lo tanto, cuando leemos ε como símbolo de entrada, entonces no debería haber nada en la pila. Por tanto el movimiento será:
δ(q1, ε, Z) = (q2, ε)
Dónde
valor java de enumeración
PDA = ({q0, q1, q2}, {a, b}, {a, Z}, δ, q0, Z, {q2})
Podemos resumir el ID como:
δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa) δ(q0, b, a) = (q1, ε) δ(q1, b, a) = (q1, ε) δ(q1, ε, Z) = (q2, ε)
Ahora simularemos esta PDA para la cadena de entrada 'aaabbbbbb'.
δ(q0, aaabbbbbb, Z) ⊢ δ(q0, aabbbbbb, aaZ) ⊢ δ(q0, abbbbbb, aaaaZ) ⊢ δ(q0, bbbbbb, aaaaaaZ) ⊢ δ(q1, bbbbb, aaaaaZ) ⊢ δ(q1, bbbb, aaaaZ) ⊢ δ(q1, bbb, aaaZ) ⊢ δ(q1, bb, aaZ) ⊢ δ(q1, b, aZ) ⊢ δ(q1, ε, Z) ⊢ δ(q2, ε) ACCEPT
Ejemplo 2:
Diseñar una PDA para aceptar un idioma 0norte1metro0norte.
Solución: En esta PDA, n números de 0 van seguidos de cualquier número de 1 seguidos de n número de 0. Por tanto, la lógica para el diseño de dicha PDA será la siguiente:
Empuja todos los 0 a la pila cuando encuentres los primeros 0. Entonces si leemos 1, simplemente no hagas nada. Luego lea 0 y, en cada lectura de 0, extraiga un 0 de la pila.
Por ejemplo:

Este escenario se puede escribir en el formulario de identificación como:
δ(q0, 0, Z) = δ(q0, 0Z) δ(q0, 0, 0) = δ(q0, 00) δ(q0, 1, 0) = δ(q1, 0) δ(q0, 1, 0) = δ(q1, 0) δ(q1, 0, 0) = δ(q1, ε) δ(q0, ε, Z) = δ(q2, Z) (ACCEPT state)
Ahora simularemos esta PDA para la cadena de entrada '0011100'.
δ(q0, 0011100, Z) ⊢ δ(q0, 011100, 0Z) ⊢ δ(q0, 11100, 00Z) ⊢ δ(q0, 1100, 00Z) ⊢ δ(q1, 100, 00Z) ⊢ δ(q1, 00, 00Z) ⊢ δ(q1, 0, 0Z) ⊢ δ(q1, ε, Z) ⊢ δ(q2, Z) ACCEPT
