Dada una matriz llegar[] que representa un Árbol binario completo es decir, si índice i es el padre índice 2*yo + 1 es el niño abandonado y índice 2*i + 2 es el niño correcto. La tarea es encontrar el mínimo numero de permutas necesaria para convertirlo en un Árbol de búsqueda binaria.
Ejemplos:
Aporte: arreglo[] = [5 6 7 8 9 10 11]
Producción: 3
Explicación:
Árbol binario de la matriz dada:

Intercambio 1: intercambie el nodo 8 con el nodo 5.
Intercambio 2: intercambie el nodo 9 con el nodo 10.
Intercambio 3: intercambie el nodo 10 con el nodo 7.Por lo tanto, se requieren un mínimo de 3 intercambios para obtener el siguiente árbol de búsqueda binaria:
boto3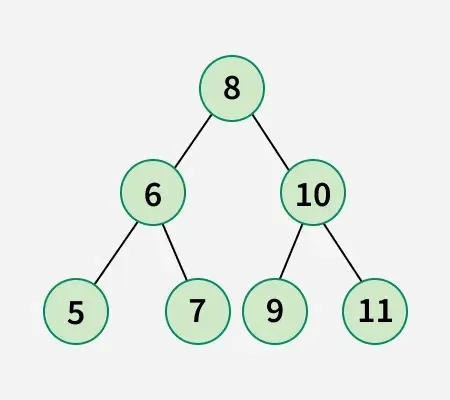
Aporte: arreglo[] = [1 2 3]
Producción: 1
Explicación:
Árbol binario de la matriz dada:alinear imagen css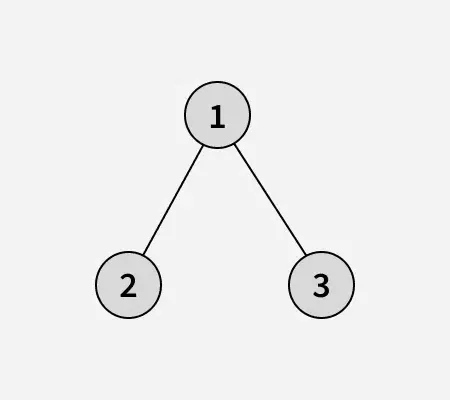
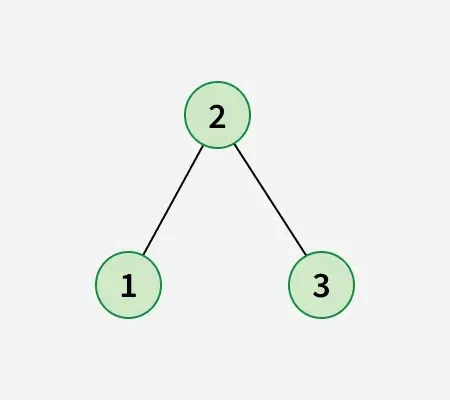
Después de intercambiar el nodo 1 con el nodo 2, obtenga el siguiente árbol de búsqueda binario:
Acercarse:
C++La idea es aprovechar el hecho de que recorrido en orden de Árbol de búsqueda binaria esta en creciente orden de su valor.
Así que encuentra el recorrido en orden del árbol binario y guárdelo en la matriz y tratar de clasificar la matriz. El número mínimo de intercambios necesarios para ordenar la matriz será la respuesta.
// C++ program for Minimum swap required // to convert binary tree to binary search tree #include
// Java program for Minimum swap required // to convert binary tree to binary search tree import java.util.Arrays; class GfG { // Function to perform inorder traversal of the binary tree // and store it in an array static void inorder(int[] arr int[] inorderArr int index int[] counter) { int n = arr.length; // Base case: if index is out of bounds return if (index >= n) return; // Recursively visit left subtree inorder(arr inorderArr 2 * index + 1 counter); // Store current node value in the inorder array inorderArr[counter[0]] = arr[index]; counter[0]++; // Recursively visit right subtree inorder(arr inorderArr 2 * index + 2 counter); } // Function to calculate minimum swaps // to sort inorder traversal static int minSwaps(int[] arr) { int n = arr.length; int[] inorderArr = new int[n]; int[] counter = new int[1]; // Get the inorder traversal of the binary tree inorder(arr inorderArr 0 counter); // Create an array of pairs to store the value // and its original index int[][] t = new int[n][2]; int ans = 0; // Store the value and its original index for (int i = 0; i < n; i++) { t[i][0] = inorderArr[i]; t[i][1] = i; } // Sort the array based on values to get BST order Arrays.sort(t (a b) -> Integer.compare(a[0] b[0])); // Find minimum swaps by detecting cycles boolean[] visited = new boolean[n]; // Iterate through the array to find cycles for (int i = 0; i < n; i++) { // If the element is already visited or in // the correct place continue if (visited[i] || t[i][1] == i) continue; // Start a cycle and find the number of // nodes in the cycle int cycleSize = 0; int j = i; while (!visited[j]) { visited[j] = true; j = t[j][1]; cycleSize++; } // If there is a cycle we need (cycleSize - 1) // swaps to sort the cycle if (cycleSize > 1) { ans += (cycleSize - 1); } } // Return the total number of swaps return ans; } public static void main(String[] args) { int[] arr = {5 6 7 8 9 10 11}; System.out.println(minSwaps(arr)); } }
# Python program for Minimum swap required # to convert binary tree to binary search tree # Function to perform inorder traversal of the binary tree # and store it in an array def inorder(arr inorderArr index): # If index is out of bounds return n = len(arr) if index >= n: return # Recursively visit left subtree inorder(arr inorderArr 2 * index + 1) # Store current node value in inorderArr inorderArr.append(arr[index]) # Recursively visit right subtree inorder(arr inorderArr 2 * index + 2) # Function to calculate minimum swaps # to sort inorder traversal def minSwaps(arr): inorderArr = [] # Get the inorder traversal of the binary tree inorder(arr inorderArr 0) # Create a list of pairs to store value and original index t = [(inorderArr[i] i) for i in range(len(inorderArr))] ans = 0 # Sort the list of pairs based on values # to get BST order t.sort() # Initialize visited array visited = [False] * len(t) # Find minimum swaps by detecting cycles for i in range(len(t)): # If already visited or already in the # correct place skip if visited[i] or t[i][1] == i: continue # Start a cycle and find the number of # nodes in the cycle cycleSize = 0 j = i # Process all elements in the cycle while not visited[j]: visited[j] = True j = t[j][1] cycleSize += 1 # If there is a cycle of size `cycle_size` we # need `cycle_size - 1` swaps if cycleSize > 1: ans += (cycleSize - 1) # Return total number of swaps return ans if __name__ == '__main__': arr = [5 6 7 8 9 10 11] print(minSwaps(arr))
// C# program for Minimum swap required // to convert binary tree to binary search tree using System; using System.Linq; class GfG { // Function to perform inorder traversal of the binary tree // and store it in an array static void Inorder(int[] arr int[] inorderArr int index ref int counter) { int n = arr.Length; // Base case: if index is out of bounds return if (index >= n) return; // Recursively visit left subtree Inorder(arr inorderArr 2 * index + 1 ref counter); // Store current node value in inorderArr inorderArr[counter] = arr[index]; counter++; // Recursively visit right subtree Inorder(arr inorderArr 2 * index + 2 ref counter); } // Function to calculate minimum // swaps to sort inorder traversal static int MinSwaps(int[] arr) { int n = arr.Length; int[] inorderArr = new int[n]; int counter = 0; // Get the inorder traversal of the binary tree Inorder(arr inorderArr 0 ref counter); // Create an array of pairs to store value // and original index var t = new (int int)[n]; for (int i = 0; i < n; i++) { t[i] = (inorderArr[i] i); } // Sort the array based on values to get BST order Array.Sort(t (a b) => a.Item1.CompareTo(b.Item1)); // Initialize visited array bool[] visited = new bool[n]; int ans = 0; // Find minimum swaps by detecting cycles for (int i = 0; i < n; i++) { // If already visited or already in // the correct place skip if (visited[i] || t[i].Item2 == i) continue; // Start a cycle and find the number // of nodes in the cycle int cycleSize = 0; int j = i; // Process all elements in the cycle while (!visited[j]) { visited[j] = true; j = t[j].Item2; cycleSize++; } // If there is a cycle of size `cycle_size` we // need `cycle_size - 1` swaps if (cycleSize > 1) { ans += (cycleSize - 1); } } // Return total number of swaps return ans; } static void Main(string[] args) { int[] arr = { 5 6 7 8 9 10 11 }; Console.WriteLine(MinSwaps(arr)); } }
// Javascript program for Minimum swap required // to convert binary tree to binary search tree // Inorder traversal to get values in sorted order function inorder(arr inorderArr index) { // If index is out of bounds return if (index >= arr.length) return; // Recursively visit left subtree inorder(arr inorderArr 2 * index + 1); // Store current node value in array inorderArr.push(arr[index]); // Recursively visit right subtree inorder(arr inorderArr 2 * index + 2); } // Function to calculate minimum swaps to sort inorder // traversal function minSwaps(arr) { let inorderArr = []; // Get the inorder traversal of the binary tree inorder(arr inorderArr 0); // Create an array of pairs to store value and original // index let t = inorderArr.map((val i) => [val i]); let ans = 0; // Sort the pair array based on values to get BST order t.sort((a b) => a[0] - b[0]); // Find minimum swaps by detecting cycles let visited = Array(arr.length) .fill(false); for (let i = 0; i < t.length; i++) { // If the element is already in the correct // position continue if (visited[i] || t[i][1] === i) continue; // Otherwise perform swaps until the element is in // the right place let cycleSize = 0; let j = i; while (!visited[j]) { visited[j] = true; j = t[j][1]; cycleSize++; } // If there is a cycle we need (cycleSize - 1) // swaps to sort the cycle if (cycleSize > 1) { ans += (cycleSize - 1); } } // Return total number of swaps return ans; } let arr = [ 5 6 7 8 9 10 11 ]; console.log(minSwaps(arr));
Producción
3
Complejidad del tiempo: O(n*logn) donde norte es el número de elementos de la matriz.
Espacio Auxiliar: O(n) porque está usando espacio adicional para la matriz
Ejercicio: ¿Podemos extender esto al árbol binario normal, es decir, un árbol binario representado mediante punteros izquierdo y derecho y no necesariamente completo?
Crear cuestionario



