Se puede utilizar una pantalla de siete segmentos para mostrar números. Dada una serie de norte números naturales. La tarea es encontrar el número en la matriz que utiliza el número mínimo de segmentos para mostrar el número. Si varios números tienen un número mínimo de segmentos, genere el número que tenga el índice más pequeño.
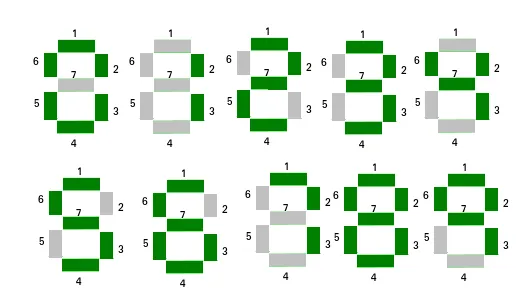
Ejemplos:
Aporte : arreglo[] = { 1 2 3 4 5 }.
Producción : 1
Explicación: El elemento que utiliza el número mínimo de segmentos es 1 (es decir, 2 segmentos)Aporte : llegada[] = { 489 206 745 123 756 }.
Producción : 745
Explicación: El elemento con el índice más pequeño que utiliza el número mínimo de segmentos es 745 (es decir, 12 segmentos).
La idea es precalcular el número de segmentos utilizados por los dígitos del 0 al 9 y almacenarlo. Ahora, para cada elemento de la matriz, sume el número de segmentos utilizados por cada dígito. Luego busque el elemento que utiliza el número mínimo de segmentos.
C++El número de segmento utilizado por dígito:
0 -> 6
1 -> 2
2 -> 5
3 -> 5
4 -> 4
5 -> 5
6 -> 6
7 -> 3
8 -> 7
9 -> 6
#include
import java.io.*; class GFG { // Precomputed values of segment // used by digit 0 to 9. static int []seg = { 6 2 5 5 4 5 6 3 7 6}; // Return the number of segments used by x. static int computeSegment(int x) { if (x == 0) return seg[0]; int count = 0; // Finding sum of the segment used by // each digit of a number. while (x > 0) { count += seg[x % 10]; x /= 10; } return count; } static int elementMinSegment(int []arr int n) { // Initialising the minimum segment // and minimum number index. int minseg = computeSegment(arr[0]); int minindex = 0; // Finding and comparing segment used // by each number arr[i]. for (int i = 1; i < n; i++) { int temp = computeSegment(arr[i]); // If arr[i] used less segment then update // minimum segment and minimum number. if (temp < minseg) { minseg = temp; minindex = i; } } return arr[minindex]; } static public void main (String[] args) { int []arr = {489 206 745 123 756}; int n = arr.length; System.out.println(elementMinSegment(arr n)); } }
# Precomputed values of segment # used by digit 0 to 9. seg = [6 2 5 5 4 5 6 3 7 6] # Return the number of # segments used by x. def computeSegment(x): if(x == 0): return seg[0] count = 0 # Finding sum of the segment # used by each digit of a number. while(x): count += seg[x % 10] x = x // 10 return count # function to return minimum sum index def elementMinSegment(arr n): # Initialising the minimum # segment and minimum number index. minseg = computeSegment(arr[0]) minindex = 0 # Finding and comparing segment # used by each number arr[i]. for i in range(1 n): temp = computeSegment(arr[i]) # If arr[i] used less segment # then update minimum segment # and minimum number. if(temp < minseg): minseg = temp minindex = i return arr[minindex] # Driver Code arr = [489 206 745 123 756] n = len(arr) # function print required answer print(elementMinSegment(arr n)) # This code is contributed by # Sanjit_Prasad
using System; class GFG{ // Precomputed values of segment // used by digit 0 to 9. static int []seg = new int[10]{ 6 2 5 5 4 5 6 3 7 6}; // Return the number of segments used by x. static int computeSegment(int x) { if (x == 0) return seg[0]; int count = 0; // Finding sum of the segment used by // each digit of a number. while (x > 0) { count += seg[x % 10]; x /= 10; } return count; } static int elementMinSegment(int []arr int n) { // Initialising the minimum segment // and minimum number index. int minseg = computeSegment(arr[0]); int minindex = 0; // Finding and comparing segment used // by each number arr[i]. for (int i = 1; i < n; i++) { int temp = computeSegment(arr[i]); // If arr[i] used less segment then update // minimum segment and minimum number. if (temp < minseg) { minseg = temp; minindex = i; } } return arr[minindex]; } static public void Main() { int []arr = {489 206 745 123 756}; int n = arr.Length; Console.WriteLine(elementMinSegment(arr n)); } }
// Precomputed values of segment // used by digit 0 to 9. let seg = [ 6 2 5 5 4 5 6 3 7 6]; // Return the number of segments used by x. function computeSegment(x) { if (x == 0) return seg[0]; let count = 0; // Finding sum of the segment used by // each digit of a number. while (x > 0) { count += seg[x % 10]; x = parseInt(x / 10 10); } return count; } function elementMinSegment(arr n) { // Initialising the minimum segment // and minimum number index. let minseg = computeSegment(arr[0]); let minindex = 0; // Finding and comparing segment used // by each number arr[i]. for(let i = 1; i < n; i++) { let temp = computeSegment(arr[i]); // If arr[i] used less segment then update // minimum segment and minimum number. if (temp < minseg) { minseg = temp; minindex = i; } } return arr[minindex]; } // Driver code let arr = [ 489 206 745 123 756 ]; let n = arr.length; console.log(elementMinSegment(arr n));
Producción
745
Complejidad del tiempo: O(n * log 10 norte)
Espacio auxiliar: O(10)
