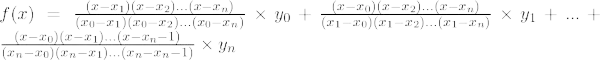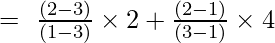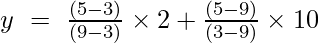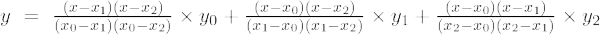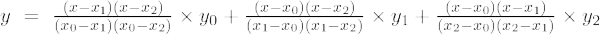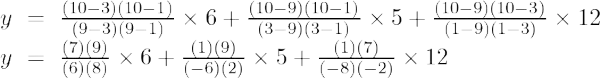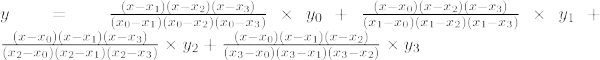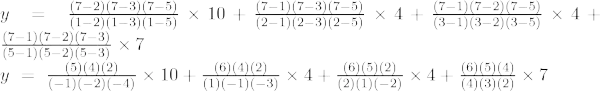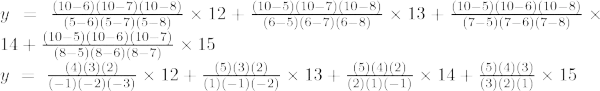logo

TechCodeview

Fórmula de interpolación de Lagrange

Fórmula de interpolación de Lagrange encuentra un polinomio llamado Polinomio de Lagrange que toma ciertos valores en un punto arbitrario. es un enésimo grado expresión polinómica de la función f(x). El método de interpolación se utiliza para encontrar nuevos puntos de datos dentro del rango de un conjunto discreto de puntos de datos conocidos.

En este artículo, aprenderemos sobre la interpolación de Lagrange, la fórmula de interpolación de Lagrange, la prueba de la fórmula de interpolación de Lagrange, ejemplos basados ​​en la fórmula de interpolación de Lagrange y otros en detalle.



¿Qué es la interpolación de Lagrange?

La interpolación de Lagrange es una forma de encontrar el valor de cualquier función en cualquier punto dado cuando la función no está dada. Usamos otros puntos de la función para obtener el valor de la función en cualquier punto requerido.

Supongamos que tenemos una función y = f(x) en la que al sustituir los valores de x se obtienen diferentes valores de y. Y nos dan dos puntos (x1, y1) y (x2, y2) en la curva, entonces el valor de y en x = a(constante) se calcula utilizando la fórmula de interpolación de Lagrange.

Fórmula de interpolación de Lagrange

Dados pocos valores reales x1, X2, X3, …, Xnortey y1, y2, y3, …, ynortey habrá un polinomio P con coeficientes reales que satisfagan las condiciones P(xi) = yi, ∀ i = {1, 2, 3,…, n} y el grado del polinomio P debe ser menor que el recuento de valores reales, es decir, grado(P)



Fórmula de interpolación de Lagrange para enésimo orden

La fórmula de interpolación de Lagrange para nthEl polinomio de grado se da a continuación:

Fórmula de interpolación de Lagrange para n th el orden es,

f(x)=frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)} imes y_0+ frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)} imes y_1+...+ frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)}veces y_n



Fórmula de interpolación de primer orden de Lagrange

Si el El grado del polinomio es 1, entonces se llama polinomio de primer orden. Fórmula de interpolación de Lagrange para 1callepolinomios de orden es,

f(x)~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

Fórmula de interpolación de segundo orden de Lagrange

Si el grado del polinomio es 2 entonces se llama polinomio de segundo orden. La fórmula de interpolación de Lagrange para polinomios de segundo orden es,

f(x)~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)} {(x_1-x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2

Prueba del teorema de Lagrange

Consideremos un polinomio de enésimo grado de la forma dada,

f(x) = A0(x-x1)(x-x2)(x-x3)…(x-xnorte) + UN1(x-x1)(x-x2)(x-x3)…(x-xnorte) + … + A(n-1)(x-x1)(x-x2)(x-x3)…(x-xnorte)

Sustituir observaciones xiconseguir uni

Poner x = x0entonces obtenemos A0

f(x)0) = y0= Un0(X0- X1)(X0- X2)(X0- X3)…(X0- Xnorte)

A 0 = y 0 /(X 0 - X 1 )(X 0 - X 2 )(X 0 - X 3 )…(X 0 - X norte )

Sustituyendo x = x1obtenemos A1

f(x)1) = y1= Un1(X1- X0)(X1- X2)(X1- X3)…(X1- Xnorte)

A 1 = y 1 /(X 1 - X 0 )(X 1 - X 2 )(X 1 - X 3 )…(X 1 - X norte )

De manera similar, sustituyendo x = xnorteobtenemos Anorte

f(x)norte) = ynorte= Unnorte(Xnorte- X0)(Xnorte- X1)(Xnorte- X2)…(Xnorte- Xn-1)

A norte = y norte /(X norte - X 0 )(X norte - X 1 )(X norte - X 2 )…(X norte - X n-1 )

Si sustituimos todos los valores de Aien la función f(x) donde i = 1, 2, 3,…n entonces obtenemos la fórmula de interpolación de Lagrange como,

f(x)~=~frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)} multiplicado por y_0+frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)} imes y_1+... +frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)} imes y_n

Propiedades de la fórmula de interpolación de Lagrange

A continuación se analizan varias propiedades de la fórmula de interpolación de Lagrange.

  • Esta fórmula se utiliza para encontrar el valor de la función en cualquier punto, incluso cuando no se proporciona la función en sí.
  • Se utiliza incluso si los puntos dados no están espaciados uniformemente.
  • Proporciona el valor de la variable dependiente de cualquier variable independiente que pertenezca a cualquier función y, por lo tanto, se utiliza en análisis numérico para encontrar los valores de la función, etc.

Usos de la fórmula de interpolación de Lagrange

A continuación se analizan varios usos de la fórmula de interpolación de Lagrange.

serie de fibonacci en java
  • Se utiliza para encontrar el valor de la variable dependiente en cualquier variable independiente particular, incluso si no se proporciona la función en sí.
  • Se utiliza en el escalado de imágenes.
  • Se utiliza en el modelado de IA.
  • Se utiliza para enseñar PNL, etc.

Leer más,

  • Fórmula de interpolación
  • Fórmula de interpolación lineal

Ejemplos que utilizan la fórmula de interpolación de Lagrange

Analicemos algunos ejemplos de preguntas sobre la fórmula de interpolación de Lagrange.

Ejemplo 1: Encuentre el valor de y en x = 2 para el conjunto de puntos dado (1, 2), (3, 4)

Solución:

Dado,

  • (X0, y0) = (1, 2)
  • (X1, y1) = (3, 4)

La fórmula de interpolación de Lagrange de primer orden es,

y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

En x = 2

y =~frac{(2-3)}{(1-3)}veces 2+frac{(2-1)}{(3-1)}veces 4

y = (-2/-2) + (4/2)

y = 1 + 2 = 3

El valor de y en x = 2 es 3

Ejemplo 2: Encuentre el valor de y en x = 5 para el conjunto dado de puntos (9, 2), (3, 10)

Solución:

Dado,

  • (X0, y0) = (9, 2)
  • (X1, y1) = (3, 10)

La fórmula de interpolación de Lagrange de primer orden es,

y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

En x = 5

y~=~frac{(5-3)}{(9-3)} imes 2+frac{(5-9)}{(3-9)} imes 10

y = (4/6) + (-40/-6)

y = (2/3) + (20/3)

y = 22/3 = 7.33

El valor de y en x = 5 es 7,33

Ejemplo 3: Encuentre el valor de y en x = 1 para el conjunto dado de puntos (1, 6), (3, 4), (2, 5)

Solución:

Dado,

  • (X0, y0) = (1, 6)
  • (X1, y1) = (3, 4)
  • (X2, y2) = (2, 5)

La fórmula de interpolación de Lagrange de segundo orden es,

y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)}{(x_1 -x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2

En x = 1

y~=~frac{(1-3)(1-2)}{(1-3)(1-2)} imes 6+frac{(1-1)(1-2)}{( 3-1)(3-2)} imes 4+frac{(1-1)(1-3)}{(2-1)(2-3)} imes 5 y~=~ frac{(-2)(-1)}{(-2)(-1)} imes 6+frac{(0)(-1)}{(2)(1)} imes 4+frac {(0)(-2)}{(1)(-1)}veces 5

y = (12/2) + 0 + 0

y = 6

El valor de y en x = 1 es 6

Ejemplo 4: Encuentre el valor de y en x = 10 para el conjunto dado de puntos (9, 6), (3, 5), (1, 12)

Solución:

Dado,

  • (X0, y0) = (9, 6)
  • (X1, y1) = (3, 5)
  • (X2, y2) = (1, 12)

La fórmula de interpolación de Lagrange de segundo orden es,

y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)}{(x_1 -x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2

En x = 10

y~=~frac{(10-3)(10-1)}{(9-3)(9-1)} imes 6+frac{(10-9)(10-1)}{( 3-9)(3-1)} imes 5+frac{(10-9)(10-3)}{(1-9)(1-3)} imes 12 y~=~ frac{(7)(9)}{(6)(8)} imes 6+frac{(1)(9)}{(-6)(2)} imes 5+frac{(1) (7)}{(-8)(-2)}veces 12

y = (63/8) + (-15/4) + (21/4)

y = (63-30 + 42)/8

y = 75/8 = 9.375

El valor de y en x = 10 es 9,375

Ejemplo 5: Encuentre el valor de y en x = 7 para el conjunto dado de puntos (1, 10), (2, 4), (3, 4), (5, 7)

Solución:

Dado,

  • (X0, y0) = (1, 10)
  • (X1, y1) = (2, 4)
  • (X2, y2) = (3, 4)
  • (X3, y3) = (5, 7)

La fórmula de interpolación de Lagrange de tercer orden es,

y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} imes y_0+frac{(x-x_0) )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} imes y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)} imes y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1 )(x_3-x_2)}veces y_3

En x = 7

y~=~frac{(7-2)(7-3)(7-5)}{(1-2)(1-3)(1-5)} imes 10+frac{(7- 1)(7-3)(7-5)}{(2-1)(2-3)(2-5)} imes 4+frac{(7-1)(7-2)(7- 5)}{(3-1)(3-2)(3-5)} imes 4+frac{(7-1)(7-2)(7-3)}{(5-1)( 5-2)(5-3)} imes 7 y~=~frac{(5)(4)(2)}{(-1)(-2)(-4)} imes 10+ frac{(6)(4)(2)}{(1)(-1)(-3)} imes 4+frac{(6)(5)(2)}{(2)(1) (-2)}veces 4+frac{(6)(5)(4)}{(4)(3)(2)}veces 7

y = -50 + 64 – 60 + 35

y = 99 – 110 = -11

El valor de y en x = 7 es -11

Ejemplo 6: Encuentre el valor de y en x = 10 para el conjunto dado de puntos (5, 12), (6, 13), (7, 14), (8, 15)

Solución:

Dado,

  • (X0, y0) = (5, 12)
  • (X1, y1) = (6, 13)
  • (X2, y2) = (7, 14)
  • (X3, y3) = (8, 15)

La fórmula de interpolación de Lagrange de tercer orden es,

y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} imes y_0+frac{(x-x_0) )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} imes y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)} imes y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1 )(x_3-x_2)}veces y_3

En x = 10,

y~=~frac{(10-6)(10-7)(10-8)}{(5-6)(5-7)(5-8)} imes 12+frac{(10- 5)(10-7)(10-8)}{(6-5)(6-7)(6-8)}veces 13+frac{(10-5)(10-6)(10- 8)}{(7-5)(7-6)(7-8)}veces 14+frac{(10-5)(10-6)(10-7)}{(8-5)( 8-6)(8-7)}veces 15 y~=~frac{(4)(3)(2)}{(-1)(-2)(-3)}veces 12+ frac{(5)(3)(2)}{(1)(-1)(-2)} imes 13+frac{(5)(4)(2)}{(2)(1) (-1)}veces 14+frac{(5)(4)(3)}{(3)(2)(1)}veces 15

y = -48 + 195 – 280 + 150

y = 17

El valor de y en x = 10 es 17

Ejemplo 7: Encuentre el valor de y en x = 0 para el conjunto de puntos dado (-2, 5), (1, 7)

Solución:

Dado,

  • (X0, y0) = (-2, 5)
  • (X1, y1) = (1, 7)

La fórmula de interpolación de Lagrange de primer orden es,

y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

En x = 0,

y~=~frac{(0-1)}{(-2-1)} imes 5+frac{(0+2)}{(1+2)} imes 7

y = (5/3) + (14/3)

y = 19/3 = 6.33

El valor de y en x = 0 es 6,33

Preguntas frecuentes sobre la fórmula de interpolación de Lagrange

1. ¿Qué es la fórmula de interpolación de Lagrange?

La fórmula de interpolación de Lagrange es una fórmula que se utiliza para encontrar el valor de la variable dependiente de la función para cualquier variable independiente, aunque no se proporcione la función en sí.

2. ¿Cuáles son las aplicaciones de la fórmula de interpolación de Lagrange?

La fórmula de Lagranges tiene diversas aplicaciones en matemáticas y ciencias de datos modernas.

  • Se utiliza para modelar AI Traning.
  • Se utiliza en el procesamiento de imágenes.
  • Se utiliza para representar gráficas en 3-D y curvas superiores, etc.

3. ¿Qué es la fórmula de interpolación de Lagrange de primer orden?

La fórmula de interpolación de Lagranges de primer orden es,

f(x) = (x – x 1 )/(X 0 - X 1 )×f 0 + (x-x 0 )/(X 1 - X 0 )×f 1

4. ¿Qué es la fórmula de interpolación de Lagrange de segundo orden?

La fórmula de interpolación de Lagranges de segundo orden es,

f(x) = [(x – x 1 )(x-x 2 )/(X 0 - X 1 )(X 0 - X 2 )]×f 0 + [(x-x 0 )(x-x 2 )/(X 1 - X 0 )(X 1 - X 2 )]×f 1 + [(x-x 0 )(x-x 1 )/(X 2 - X 0 )(X 2 - X 2 )]×f 0