A Gráfico Acíclico Dirigido , a menudo abreviado como DÍA , es un concepto fundamental en la teoría de grafos. DAG Se utilizan para mostrar cómo las cosas se relacionan o dependen unas de otras de una manera clara y organizada. En este artículo vamos a aprender sobre Gráfico Acíclico Dirigido , sus propiedades y aplicación en la vida real.

Gráfico Acíclico Dirigido

¿Qué es el gráfico acíclico dirigido?

A Gráfico acíclico dirigido (DAG) es un gráfico dirigido que no contiene ningún ciclo.

El siguiente gráfico representa un gráfico acíclico dirigido (DAG):

Gráfico acíclico directo

Significado del gráfico acíclico dirigido:

El gráfico acíclico dirigido tiene dos características importantes:

• Borde dirigido s:En gráfico acíclico dirigido, cada arista tiene una dirección, es decir, va de un vértice (nodo) a otro. Esta dirección significa una Un camino relación o dependencia entre nodos.
• Acíclico: El término acíclico indica que no hay ciclos ni bucles cerrados dentro del gráfico. En otras palabras, no se puede atravesar una secuencia de aristas dirigidas y regresar al mismo nodo, siguiendo las direcciones de las aristas. La formación de ciclos está prohibida en DÍA. De ahí que esta característica sea esencial.

Gráfico Acíclico Dirigido

Propiedades del gráfico acíclico dirigido DAG:

El gráfico acíclico dirigido (DAG) tiene diferentes propiedades que los hacen utilizables en problemas de gráficos.

Existen las siguientes propiedades del gráfico acíclico dirigido (DAG):

• Relación de Accesibilidad: En DAG, podemos determinar si existe una relación de accesibilidad entre dos nodos. Se dice que el nodo A es accesible desde el nodo B si existe una ruta dirigida que comienza en el nodo B y termina en el nodo A. Esto implica que puede seguir la dirección de los bordes en el gráfico para ir de B a A.
• Clausura transitiva: El cierre transitivo de un gráfico dirigido es un nuevo gráfico que representa todas las relaciones o conexiones directas e indirectas entre nodos en el gráfico original. En otras palabras, le indica a qué nodos se puede llegar desde otros nodos siguiendo uno o más bordes dirigidos.

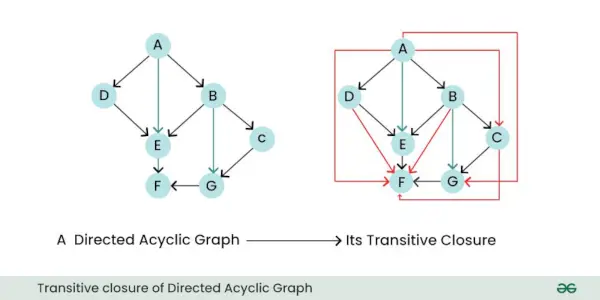
Cierre transitivo de gráfico acíclico dirigido

• Reducción transitiva: La reducción transitiva de un gráfico dirigido es un nuevo gráfico que conserva solo las relaciones directas esenciales entre los nodos, al tiempo que elimina los bordes indirectos innecesarios. En esencia, simplifica el gráfico eliminando los bordes que se pueden inferir de los bordes restantes.

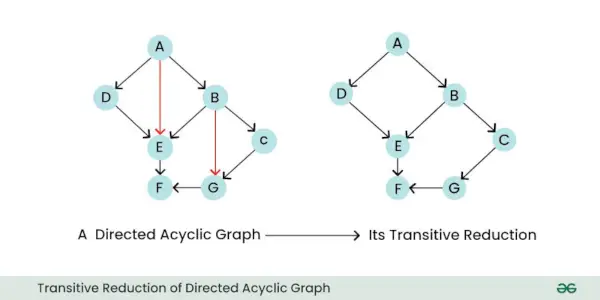
Reducción transitiva del gráfico acíclico dirigido

• Ordenamiento topológico: Un DAG se puede ordenar topológicamente, lo que significa que puede ordenar linealmente sus nodos de tal manera que para todos los bordes, el nodo inicial del borde ocurra antes en la secuencia. Esta propiedad es útil para tareas como programación y resolución de dependencias.

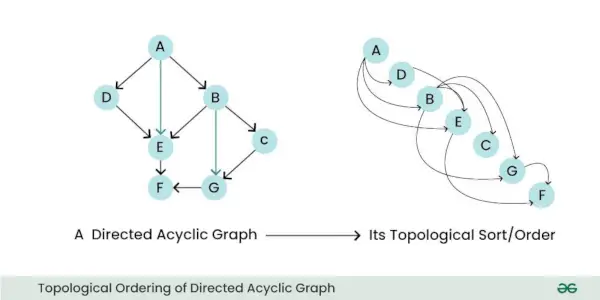
Ordenamiento topológico del gráfico acíclico dirigido

Aplicaciones prácticas de DAG:

• Análisis de flujo de datos: En el diseño y optimización del compilador, los DAG se utilizan para representar el flujo de datos dentro de un programa. Esto ayuda a optimizar el código al identificar cálculos redundantes y código inactivo. Los DAG también se utilizan para representar la estructura de bloques basicos en Diseño de compiladores.

• Programación de tareas: Los DAG se utilizan en la gestión de proyectos y la programación de trabajos. Cada tarea o trabajo se representa como un nodo en el DAG, con bordes dirigidos que indican dependencias. La naturaleza acíclica del DAG garantiza que las tareas se programen en un orden lógico, evitando dependencias circulares.

Se puede utilizar un gráfico acíclico dirigido ponderado para representar un problema de programación. Tomemos el ejemplo de un problema de programación de tareas. Aquí, un vértice puede representar la tarea y su peso puede representar el tamaño del cálculo de la tarea. De manera similar, una ventaja puede representar la comunicación entre dos tareas y su peso puede representar el costo de la comunicación:

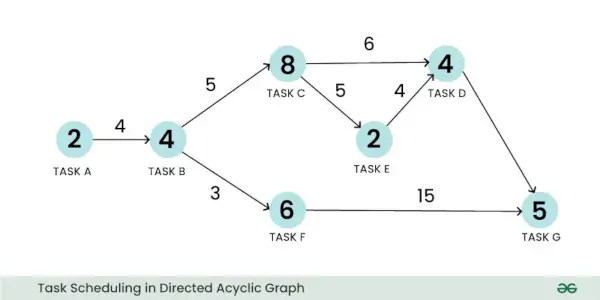
Programación de tareas en gráfico acíclico dirigido

Conclusión:

En resumen, los grafos acíclicos dirigidos son un concepto fundamental de la teoría de grafos con numerosas aplicaciones prácticas. Los DAG desempeñan un papel crucial en la programación de tareas, el análisis del flujo de datos, la resolución de dependencias y varias otras áreas de la informática y la ingeniería. Ayudan a optimizar procesos, gestionar dependencias y garantizar la ejecución eficiente de tareas o trabajos.