El mundo algorítmico es hermoso, con múltiples estrategias y herramientas que se desarrollan las 24 horas del día para satisfacer la necesidad de computación de alto rendimiento. De hecho, cuando los algoritmos se inspiran en leyes naturales se observan resultados interesantes. Los algoritmos evolutivos pertenecen a esta clase de algoritmos. Estos algoritmos están diseñados para imitar ciertos comportamientos, así como rasgos evolutivos del genoma humano. Además, este diseño algorítmico no sólo está restringido a los humanos, sino que también puede inspirarse en el comportamiento natural de ciertos animales. El objetivo básico de fabricar tales metodologías es proporcionar soluciones realistas, relevantes y, sin embargo, de bajo costo a problemas que hasta ahora no pueden resolverse por medios convencionales.

Así, a partir de estos algoritmos evolutivos han evolucionado diferentes técnicas de optimización, abriendo así el dominio de las metaheurísticas. metaheurística se deriva de dos palabras griegas, a saber, Meta significado un nivel arriba y heuriskein significado encontrar . Algoritmos como la optimización de enjambre de partículas (PSO) y la optimización de colonias de hormigas (ACO) son ejemplos de metaheurística e inteligencia de enjambre. El objetivo de la inteligencia de enjambre es diseñar sistemas inteligentes multiagente inspirándose en el comportamiento colectivo de insectos sociales como hormigas, termitas, abejas, avispas y otras sociedades animales como bandadas de pájaros o bancos de peces.

Fondo:

La técnica de optimización de colonias de hormigas está puramente inspirada en forrajeando comportamiento de las colonias de hormigas, introducido por primera vez por Marco Dorigo en la década de 1990. Las hormigas son insectos eusociales que prefieren la supervivencia y el sustento comunitarios en lugar de ser especies individuales. Se comunican entre sí mediante sonido, tacto y feromonas. Feromonas Son compuestos químicos orgánicos secretados por las hormigas que desencadenan una respuesta social en miembros de una misma especie. Se trata de sustancias químicas capaces de actuar como hormonas fuera del cuerpo del individuo que las secreta, para impactar el comportamiento de los individuos que las reciben. Dado que la mayoría de las hormigas viven en el suelo, utilizan la superficie del suelo para dejar rastros de feromonas que otras hormigas pueden seguir (oler).
Las hormigas viven en nidos comunitarios y el principio subyacente de ACO es observar el movimiento de las hormigas desde sus nidos para buscar alimento en el camino más corto posible. Inicialmente, las hormigas comienzan a moverse aleatoriamente en busca de alimento alrededor de sus nidos. Esta búsqueda aleatoria abre múltiples rutas desde el nido hasta la fuente de alimento. Ahora, dependiendo de la calidad y cantidad del alimento, las hormigas transportan una porción del mismo con la concentración necesaria de feromonas en su camino de regreso. Dependiendo de estas pruebas de feromonas, la probabilidad de que las siguientes hormigas seleccionen un camino específico sería un factor guía hacia la fuente de alimento. Evidentemente, esta probabilidad se basa tanto en la concentración como en la tasa de evaporación de la feromona. También se puede observar que, dado que la tasa de evaporación de la feromona también es un factor decisivo, la longitud de cada camino puede calcularse fácilmente.

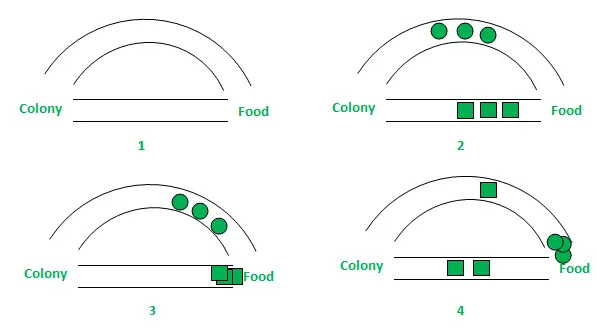
En la figura anterior, por simplicidad, sólo se han considerado dos caminos posibles entre la fuente de alimento y el hormiguero. Las etapas se pueden analizar de la siguiente manera:

Etapa 1: Todas las hormigas están en su nido. No hay contenido de feromonas en el medio ambiente. (Para el diseño algorítmico, la cantidad de feromonas residuales se puede considerar sin interferir con la probabilidad) Etapa 2: Las hormigas comienzan su búsqueda con la misma probabilidad (0,5 cada una) a lo largo de cada camino. Claramente, el camino curvo es el más largo y, por lo tanto, el tiempo que tardan las hormigas en llegar a la fuente de alimento es mayor que el otro. Etapa 3: Las hormigas por el camino más corto llegan antes a la fuente de alimento. Ahora, evidentemente, se enfrentan a un dilema de selección similar, pero esta vez debido al rastro de feromonas a lo largo del camino más corto ya disponible, la probabilidad de selección es mayor. Etapa 4: Más hormigas regresan por el camino más corto y posteriormente también aumentan las concentraciones de feromonas. Además, debido a la evaporación, la concentración de feromonas en el camino más largo se reduce, disminuyendo la probabilidad de selección de este camino en etapas posteriores. Por lo tanto, toda la colonia utiliza gradualmente el camino más corto en probabilidades más altas. Por lo tanto, se logra la optimización de la ruta.

Diseño algorítmico:

interfaz vs clase abstracta

En relación con el comportamiento anterior de las hormigas, ahora se puede desarrollar un diseño algorítmico. Para simplificar, se ha considerado una única fuente de alimento y una única colonia de hormigas con sólo dos caminos de posible recorrido. Todo el escenario se puede realizar a través de gráficos ponderados donde la colonia de hormigas y la fuente de alimento actúan como vértices (o nodos); los caminos sirven como bordes y los valores de feromonas son los pesos asociados con los bordes.
Sea la gráfica GRAMO = (V, mi) donde V, E son las aristas y los vértices del gráfico. Los vértices según nuestra consideración son EN_s (Vértice de origen – colonia de hormigas) y EN_d (Vértice de destino – Fuente de alimento), Los dos bordes son Y₁ y Y₂ con longitudes l₁ y l₂ asignado a cada uno. Ahora bien, se puede suponer que los valores de feromonas asociados (indicativos de su fuerza) son R₁ y R₂ para vértices E₁y E₂respectivamente. Así, para cada hormiga, la probabilidad inicial de selección del camino (entre E₁y E₂) se puede expresar de la siguiente manera:

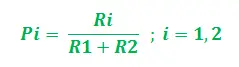
Evidentemente, si R₁>R₂, la probabilidad de elegir E₁es mayor y viceversa. Ahora, mientras regresa por este camino más corto, diga E._i, el valor de feromona se actualiza para la ruta correspondiente. La actualización se realiza en función de la longitud de los caminos y de la tasa de evaporación de la feromona. Por lo tanto, la actualización se puede realizar paso a paso de la siguiente manera:

Según la longitud del camino –

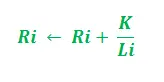
En la actualización anterior, i = 1, 2 y 'K' sirve como parámetro del modelo. Además, la actualización depende de la longitud del camino. Cuanto más corto sea el camino, mayor será la feromona añadida. De acuerdo con la tasa de evaporación de la feromona –

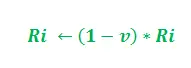
El parámetro 'v' pertenece al intervalo (0, 1] que regula la evaporación de feromonas. Además, i = 1, 2.

En cada iteración, todas las hormigas se colocan en el vértice fuente V._s(colonia de hormigas). Posteriormente, las hormigas se mueven de V_sa V_d(fuente de alimento) siguiendo el paso 1. A continuación, todas las hormigas realizan su viaje de regreso y refuerzan el camino elegido según el paso 2.

diferencia entre hielo y nieve

Pseudocódigo:

 Procedure AntColonyOptimization: Initialize necessary parameters and pheromone trials; while not termination do : Generate ant population; Calculate fitness values associated with each ant; Find best solution through selection methods; Update pheromone trial; end while end procedure>

La actualización de feromonas y los cálculos de aptitud en el pseudocódigo anterior se pueden encontrar a través de las implementaciones paso a paso mencionadas anteriormente.
Así, se ha establecido la introducción de la técnica de optimización ACO. La aplicación del ACO se puede extender a diversos problemas como el famoso TSP (Problema del viajante) .

Referencias:
https://www.ics.uci.edu/~welling/teaching/271fall09/antcolonyopt.pdf