Incentro de un triángulo es el punto de intersección de las tres bisectrices de un triángulo. El incentro es un punto importante en un triángulo donde se juntan las líneas que cortan ángulos por la mitad. Este punto es también el centro de un círculo llamado Incircle que encaja perfectamente dentro del triángulo y toca los tres lados por igual. Este artículo cubre varios conceptos del incentro del triángulo, como por qué este punto es importante, cómo encontrarlo usando un compás o números y las propiedades del incentro del círculo.
Tabla de contenidos
- ¿Qué es el incentro de un triángulo?
- Propiedades de un incentro de un triángulo
- Fórmula del incentro de un triángulo
- Cómo encontrar el incentro de un triángulo
- Centroide, Circuncentro, Incentro, Ortocentro
¿Qué es el incentro de un triángulo?
El incentro de un triángulo, como su nombre indica, es el punto central del triángulo. Este punto que llamamos incentro se forma en la unión donde se encuentran todas las líneas que bisecan los ángulos internos. La distancia del punto a los tres lados del triángulo es la misma. El círculo interior del triángulo también encaja en un círculo perfecto dentro del triángulo y este círculo se llama círculo interior del triángulo.
Definición de incentro
El incentro de un triángulo es el punto dentro del triángulo donde se juntan las tres líneas que cortan sus ángulos interiores por la mitad. Este punto está a la misma distancia de los tres lados del triángulo, lo que lo convierte en el centro del triángulo. También es el centro del círculo más grande que puede caber perfectamente dentro del triángulo, al que llamamos círculo interior. Para simbolizar el incentro, normalmente usamos la letra I,
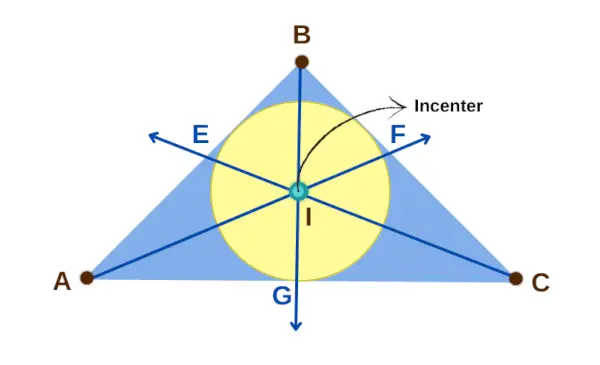
Incentro de un triángulo
Propiedades de un incentro de un triángulo
Algunas propiedades importantes del incentro del triángulo se dan a continuación:
Propiedad 1: Si I es el incentro de un triángulo ABC, entonces tres pares de segmentos de recta tienen la misma longitud: AE y AG, CG y CF, y BF y BE. Esto significa que AE = AG, CG = CF y BF = BE.
Propiedad 2: el incentro I También tiene una relación especial con los ángulos del triángulo. Hace que los ángulos ∠BAI y ∠CAI sean iguales, ∠BCI y ∠ACI sean iguales y ∠ABI y ∠CBI sean iguales. Esto sigue el teorema de la bisectriz del ángulo.
Propiedad 3: el incentro I es el centro de un círculo que toca los tres lados del triángulo, y las distancias desde I a los lados del triángulo (EI, FI, GI) son todos iguales. Estas distancias se llaman inradios o radio del círculo.
Propiedad 4: Puedes calcular el área del triángulo usando el semiperímetro (s) y el inradio (r). La fórmula es A = sr, donde A es el área, s es el semiperímetro (s = (a + b + c)/2, donde a, b y c son las longitudes de los lados del triángulo) y r es la radio.
Propiedad 5: El incentro de un triángulo siempre queda dentro del triángulo. A diferencia del ortocentro, que en algunos casos puede estar fuera del triángulo, el incentro siempre está contenido dentro de los límites del triángulo.
Fórmula del incentro de un triángulo
La fórmula para encontrar el incentro de la fórmula con 3 coordenadas (x1, y1), (X2, y2), y (x3, y3) es:
{(hacha 1 + bx 2 + cx 3 )/(a + b + c), (es 1 + por 2 +c 3 )/(a + b + c)}
En términos simples, para obtener el incentro, usted:
- Multiplica la coordenada x del punto A por la longitud del lado a, la coordenada x del punto B por la longitud del lado b y la coordenada x del punto C por la longitud del lado c. Luego, súmelos.
- Divide el resultado por la suma de las longitudes de los lados a, b y c.
- Repita el mismo proceso para las coordenadas y, pero usando las longitudes de los lados a, by c.
Fórmula del incentro del ángulo de un triángulo
La fórmula para encontrar el incentro de un ángulo de un triángulo es la siguiente:
Sean, en un triángulo D, F y G, los puntos donde las bisectrices de los ángulos A, B y C respectivamente, cortan los lados BC, AC y AB.
El ángulo ∠AIB (donde I es el incentro del triángulo) se puede calcular mediante la fórmula:
∠AIB = 180° – (la mitad de la suma de los ángulos A y B)
O
∠AIB = 180° – (∠A + ∠B)/2
Cómo encontrar el incentro de un triángulo
Hay dos métodos para encontrar el incentro de un triángulo. En construcción, localizamos el incentro dibujando las bisectrices del ángulo del triángulo. En geometría de coordenadas, empleamos una fórmula para determinar el incentro.
Usando geometría de coordenadas : Encuentra el incentro del triángulo con las coordenadas dadas como: A(2, 2), B(6, 2) y C(4, 5)
Según la información dada
- (X1, y1) = (2, 2)
- (X2, y2) = (6, 2)
- (X3, y3) = (4, 5)
Sabemos que el incentro de un triángulo es:
mi grillo vivo en
I(x, y) = {(hacha 1 + bx 2 + cx 3 )/(a + b + c), (es 1 + por 2 +c 3 )/(a + b + c)}
Para el lado a: La distancia entre los puntos B y C = √((6 – 4)2+ (2 – 5)2) = √8
Para el lado b: La distancia entre los puntos A y C = √((2 – 4)2+ (2 – 5)2) = √13
Para el lado c: La distancia entre los puntos A y B = √((6 – 2)2+ (2 – 2)2) = 4
Poniendo los valores de a, b, c en la fórmula del incentro, obtenemos:
I(x, y) = {(8×2 + 13×5 + 4×4)/(8 + 13 +4), (8×2 + 13×2 + 4×5)/(8 + 13 +4)}
⇒ I(x, y) = (16 + 78 + 16)/(25), (16 + 26 + 20)/(25)
⇒ I(x, y) = (110/25, 62/25) = (22/5,62/25)
∴ El incentro del triángulo ABC de coordenadas es (22/5,62/25)
¿Cómo construir el incentro de un triángulo?
Para construir el incentro de un triángulo será necesario utilizar un compás. Usando una brújula, siga los pasos que se indican a continuación:
Paso 1: Pon un extremo del compás en un vértice del triángulo y el otro extremo toca un lado.
Paso 2: Usa el compás para dibujar dos arcos en dos lados del triángulo.
Paso 3: Con la misma distancia en el compás, traza dos arcos dentro del triángulo. Estos arcos deben cruzarse desde donde tocan los lados.
Etapa 4: Dibuja una línea desde el vértice del triángulo hasta donde se cruzan los dos arcos interiores.
Paso 5: Repite los mismos pasos desde el otro vértice del triángulo.
Paso 6: Donde las dos líneas se encuentran o se cruzan es el incentro del triángulo.
Incentro de un triángulo rectángulo
El incentro si un Triángulo rectángulo es el punto donde se encuentran todas las bisectrices de un triángulo rectángulo. Si los lados de un triángulo rectángulo miden a, b y c, entonces el radio del círculo 'r' se da como r = (ab)/(a + b + c). El incentro del triángulo rectángulo se ilustra a continuación:
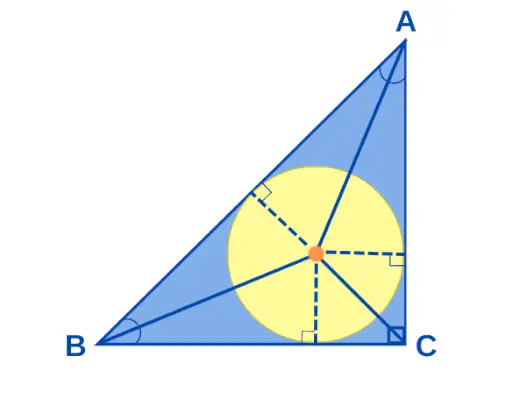
Incentro de un triángulo rectángulo
Centroide, Circuncentro, Incentro, Ortocentro
Centroide, Circuncentro, Incentro y Ortocentro son los cuatro puntos importantes relacionados con un trengle. A continuación se tabula una comparación entre centroide, circuncentro, incentro y ortocentro:
centroide | alrededor del centro | En el centro | Ortocentro |
|---|---|---|---|
Punto de intersección de la mediana | Punto de intersección de la bisectriz perpendicular | Punto de intersección de la bisectriz del ángulo | Punto de intersección de altitudes |
Divide la mediana en 2:1 | Centro del círculo circunstante del triángulo | Centro de la circunferencia del triángulo | El ortocentro del triángulo rectángulo está en ángulo recto. |
Además, consulte
- Área del Triángulo
- Perímetro del triángulo
- Propiedad de la suma de ángulos de un triángulo
Ejemplos de incentro de un triángulo
Ejemplo 1: Calcular el incentro del triángulo ABC. AB= 8cm, BC= 15cm, CA= 17cm.
Solución:
Usando la fórmula del Incentro del Triángulo = (aA + bB + cC)/(a + b + c)
dónde,
- un = 8
- segundo = 15
- c = 17
Y los ángulos son,
- A = 30°
- B = 60°
- C = 90°
Poniendo estos valores en la fórmula para obtener,
⇒ {(8)(30) + (15)(60) + (17)(90)}/{8 + 15 + 17}
⇒ (240 + 900 + 1530)/40
⇒ 2670/40
⇒ 66.75
Ejemplo 2: Jane calculó el área de un campo triangular en 120 metros cuadrados. El perímetro del campo es de 36 metros. Si se dibuja un círculo dentro del triángulo de manera que toque cada lado del triángulo, ayuda a Jane a calcular el inradio del triángulo.
Solución:
Según la información dada,
Área del triángulo = 120 metros cuadrados
Perímetro del triángulo = 36 metros
Sabemos que el área de un triángulo = r × s
s = semiperimeter
s = p/2 = 36/2 = 18
A = r×s
r = A/s
r = 120/18
r = 6,67 metros
Problemas de práctica sobre el incentro de un triángulo
Problema 1: Dado el triángulo PQR con vértices P(1, 2), Q(4, 6) y R(7, 2), encuentre las coordenadas del incentro.
Problema 2: Construya un triángulo ABC con ∠A = 45°, ∠B = 60° y ∠C = 75°. Utilice el método de construcción para encontrar el incentro.
Problema 3: En el triángulo LMN, si ∠L = 75°, ∠M = 60° y ∠N = 45°, encuentra las coordenadas del incentro.
Problema 4: Construya un triángulo XYZ con ∠X = 80°, ∠Y = 50° y ∠Z = 50°. Utilice el método de construcción para encontrar el incentro.
Incentro de un triángulo: preguntas frecuentes
¿Qué es el incentro de un triángulo?
El incentro de un triángulo es el punto donde se cortan las bisectrices de los ángulos interiores. Es equidistante de los tres lados del triángulo.
¿Cuál es el significado del incentro en un triángulo?
El incentro es significativo ya que es el centro del círculo interior del triángulo, el círculo más grande que cabe dentro del triángulo. Tiene la propiedad de ser equidistante de todos los lados.
¿Puede el incentro estar fuera del triángulo?
No, el incentro siempre está dentro del triángulo. Es el punto de concurrencia de las bisectrices de los ángulos y, por definición, debe estar dentro de los límites del triángulo.
¿Cómo se construye el Incenter utilizando un compás y una regla?
Para construir el incentro, usa un compás para dibujar bisectrices desde cada vértice hacia el lado opuesto. El incentro es el punto donde se cruzan estas bisectrices.
¿Qué es la fórmula Incenter?
La fórmula del incentro de un triángulo se puede escribir como:
frac{(aA+bB+cC)}{a+b+c}
¿Cuáles son las propiedades del incentro de un triángulo?
El incentro tiene algunas propiedades clave. Está equidistante de los lados del triángulo, lo que significa que las distancias a los lados son iguales. Además, es el punto de intersección de las bisectrices de los ángulos, dividiendo los ángulos en dos partes iguales.
¿Cómo se determina el incentivo?
Para determinar el incentro, necesitas encontrar dónde se cruzan las bisectrices de los ángulos. Esto se puede hacer usando la fórmula del incentro o dibujando las bisectrices de los ángulos y encontrando su punto de intersección.
¿Cuál es la diferencia entre incentro y circuncentro?
La principal diferencia entre el incentro y el circuncentro es su enfoque. El incentro trata de las bisectrices de un ángulo y es el centro del círculo inscrito, mientras que el circuncentro trata de las bisectrices perpendiculares y es el centro del círculo circunscrito.
¿Incentre y Centroid son iguales?
No, el incentro y el centroide son diferentes. El incentro es donde se encuentran las bisectrices de los ángulos, mientras que el centroide es donde se cruzan las medianas. Las medianas conectan los vértices con el punto medio del lado opuesto.
¿Incentre y Orthocentre son lo mismo?
No, el incentro y el ortocentro no son lo mismo. El incentro es el punto donde los ángulos se bisecan, mientras que el ortocentro implica altitudes: líneas desde cada vértice perpendiculares al lado opuesto. Son diferentes puntos de un triángulo.
