La altura o profundidad de un árbol binario se puede definir como el número máximo o mayor de bordes desde un nodo hoja hasta el nodo raíz o desde un nodo raíz hasta el nodo hoja. El nodo raíz estará en el nivel cero, lo que significa que si el nodo raíz no tiene ninguno de los nodos secundarios conectados, entonces se dice que la altura o profundidad del árbol binario en particular es cero.
Tomemos un ejemplo para comprender mejor la altura del árbol binario.
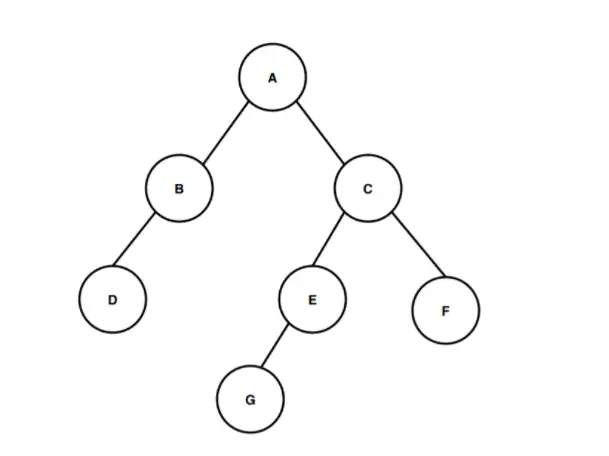
En la imagen de arriba, tenemos un árbol binario que comienza desde el nodo raíz llamado A. El nodo raíz A tiene dos nodos secundarios B y C como hijo izquierdo y derecho respectivamente. Y de manera similar, el nodo hijo izquierdo B tiene solo un nodo hijo izquierdo llamado D y el nodo hijo derecho C tiene dos nodos hijos E y F, de los cuales el nodo E tiene el nodo G como único hijo izquierdo.
ups
Ahora calculemos la altura de este árbol binario. Cuente el número de aristas desde el nodo raíz hasta el nodo de hoja más profundo para calcular la altura del árbol binario. El nodo más profundo que está presente en este árbol binario es el nodo G. Entonces, para calcular la altura o profundidad de este árbol binario necesitamos calcular el número de aristas entre el nodo raíz y el nodo más profundo G. El primer arista es del nodo A al nodo C, el segundo borde es del nodo C al nodo E y el tercer borde es del nodo E al nodo G. Entonces, para atravesar desde el nodo raíz A hasta el nodo más profundo G hay tres bordes , por lo que la altura o profundidad del árbol binario es 3. El camino que seguimos para pasar de la raíz al nodo hoja más profundo es A > C > E > G y este camino cubre tres aristas durante el recorrido, es por eso que según Según la definición de la altura del árbol binario, la altura de este árbol binario es 3.
Formas de encontrar la altura del árbol binario
Ahora, escribamos código para encontrar la altura de un árbol binario. Hay dos formas de encontrar la altura del árbol binario. uno es el método recursivo y el otro es el método no recursivo que hará uso de la estructura de datos de la cola para calcular la altura del árbol binario.
Manera recursiva
Primero, veamos la forma recursiva de encontrar la altura del árbol binario.
Código:
// Java program to create and to find the height of a binary tree by recursive way // util package is imported to use classes like Queue and LinkedList import java.util.*; // A class named Node is created representing a single node of a binary tree class Node{ // The class Node has three class variables named key and left and right of int type and Node type respectively. // the key variable holds the actual value that is assigned to that node of the binary tree int key; // left and right variables that are of Node type will be used to store the left and right child nodes of the parent of the binary tree Node left, right; // a parameterized constructor is created to create and add data to the node at the same time. public Node(int item) { key = item; left = right = null; } } // end of node class definition // A public class named BinaryTree is created having two constructors and methods to print the binary tree level-wise. class BinaryTree{ // A static variable named root_node is created that will represent the node of the binary tree static Node root_node; // A parametrized constructor of the BinaryTree class is written having the key as a parameter BinaryTree(int key) { // here we are constructing a new node and assigning it to the root node root_node = new Node(key); } BinaryTree() { root_node = null; } // a public static function named print tree is created to print all the nodes in the tree level-wise starting from the root node public static void printTree() { int h = height(root_node); int i; for (i=1; i<=h; i++){ printcurrentlevel(root_node, i); system.out.println(); } a public static function named height is created to fund the of binary tree starting from root node deepest leaf that present in passed as parameter called recursively until returned null find int height(node root){ then will be zero if (root="=" null) return 0; else { * compute each subtree lheight="height(root.left);" rheight="height(root.right);" use larger one both sub trees calcualted and which higher used. (lheight> rheight) return(lheight+1); else return(rheight+1); } } // a Public static function named printCurrentLevel is created to print al the nodes that are present in that level // this function is called repeatedly for each level of the binary tree to print all the nodes in that particular level public static void printCurrentLevel (Node root ,int level) { if (root == null) return; if (level == 1) System.out.print(root.key + ' '); else if (level > 1) { printCurrentLevel(root.left, level-1); printCurrentLevel(root.right, level-1); } } //the main function is created to create an object of the BinaryTree class and call the printTree method to level-wise print the nodes of the binary tree and the height method to find the height of the binary tree public static void main(String[] args){ // first of all we have created an Object of the BinaryTree class that will represent the binary tree BinaryTree tree = new BinaryTree(); // now a new node with the value as 150 is added as the root node to the Binary Tree tree.root_node = new Node(150); // now a new node with the value 250 is added as a left child to the root node tree.root_node.left = new Node(250); // now a new node with the value 270 is added as a right child to the root node tree.root_node.right = new Node(270); // now a new node with the value 320 is added as a left child to the left node of the previous level node tree.root_node.left.left = new Node(320); // now a new node with the value 350 is added as a right child to the right node of the previous level node tree.root_node.left.right = new Node(350); /* 150 / 250 270 / / 320 350 null null */ System.out.println('Printing the nodes of tree level wise :'); System.out.println('Level order traversal : '); tree.printTree(); // height of the binary tree is calculated bypassing the root as parameter to the height() function. int h = tree.height(tree.root_node) System.out.println('The height of the Binary tree is : ' + h ); } } // end of the BinaryTree class </=h;> Producción: La salida del código anterior es:
Printing the nodes of tree level wise: Level order traversal: (level 0) 150 (level 1) 250 270 (level 2) 320 350 The height of the Binary tree is: 2
De forma recursiva hemos llamado a la altura() funcione repetidamente para encontrar la altura del árbol binario. El nodo raíz del árbol binario se pasa como parámetro a la función height(). La función height() calcula la altura de ambos subárboles del nodo raíz y cuál de las dos alturas es mayor se considera como la altura del árbol binario.
Manera no recursiva
Ahora veamos la forma no recursiva de encontrar la altura del árbol binario.
Código:
// A C++ program to create and to find the height of a binary tree by non recursive way // iostream header file is included to use the cin and cout objects of the istream and ostream classes respectively #include #include using namespace std; // A struct named Node is created representing a single node of a binary tree struct Node { // The struct Node has three variables named key and left and right of int type and Node type respectively. // the key variable holds the actual value that is assigned to that node of the binary tree int key; // left and right variables that are of Node type will be used to store the left and right child nodes of the parent of the binary tree struct Node* left, *right; }; // A Function named newNode is created to add a new node to the binary tree, the newNode function has one parameter of integer type named key that will represent the value that particular new node will be storing Node* newNode(int key) { Node* temp = new Node; temp->key = key; temp->left = temp->right = NULL; return (temp); } // A function named height is created to find the height of the binary tree with non recursive way // The parameter to the height function is the root node of the binary tree that will be present at level zero // In the height function the nodes of the binary tree are added into the Queue data structure and the depth variable is incremented until // the NULL node is encountered while traversing the nodes of the binary tree stored in the Queue data structure. int height(struct Node* root){ //Initialising a variable to count the //height of tree int depth = 0; queueq; //Pushing first level element along with NULL q.push(root); q.push(NULL); while(!q.empty()){ Node* temp = q.front(); q.pop(); //When NULL encountered, increment the value if(temp == NULL){ depth++; } //If NULL not encountered, keep moving if(temp != NULL){ if(temp->left){ q.push(temp->left); } if(temp->right){ q.push(temp->right); } } //If queue still have elements left, //push NULL again to the queue. else if(!q.empty()){ q.push(NULL); } } return depth; } // Start of the main function int main() { // first of all we have created an Object of the struct Node that will represent the binary tree // the value of the root node is 10 Node *root = newNode(10); // now a new node with the value 20 is added as a left child to the root node root->left = newNode(20); // now a new node with the value 30 is added as a right child to the root node root->right = newNode(30); // now a new node with the value 40 is added as a left child to the left node of the previous level node root->left->left = newNode(40); // now a new node with the value 50 is added as a right child to the left node of the previous level node root->left->right = newNode(50); /* 10 / 20 30 / / 40 50 null null */ cout<<'the height(depth) of tree is: '<<height(root); cout<<endl; } end the main function < pre> <p> <strong>Output:</strong> </p> <pre> The Height(Depth) of the tree is: 2 </pre> <p>In this approach, we have used a non recursive way to find the depth of the binary tree. To find the height of the binary tree, we have written a function named height that will require a parameter of Node type (that means the root of the binary tree whose height needs to be calculated). The root of the binary tree is present at level zero, which means the height or depth of the root is zero.</p> <p>In the non recursive approach, we use the Queue Data Structure to find the depth of the binary tree. The nodes of the binary tree for which we want to find the depth are added to the Queue data structure with the help of an enqueue operation to which the node of the binary tree is passed as a parameter to this function.</p> <p>Once all the nodes are added to the queue, the nodes added in the queue are removed by calling the dequeue function that will keep on removing one element from the queue until the null node of the binary tree is encountered. Each time a node of the binary tree from the queue is removed, the depth variable representing the depth of the binary tree is incremented by one. And in the end, the value of the depth variable will represent the final depth of the binary tree.</p> <hr></'the> En este enfoque, hemos utilizado una forma no recursiva para encontrar la profundidad del árbol binario. Para encontrar la altura del árbol binario, hemos escrito una función llamada altura que requerirá un parámetro de tipo Nodo (es decir, la raíz del árbol binario cuya altura debe calcularse). La raíz del árbol binario está presente en el nivel cero, lo que significa que la altura o profundidad de la raíz es cero.
En el enfoque no recursivo, utilizamos la estructura de datos de cola para encontrar la profundidad del árbol binario. Los nodos del árbol binario cuya profundidad queremos encontrar se agregan a la estructura de datos de la cola con la ayuda de una operación de puesta en cola a la que se pasa el nodo del árbol binario como parámetro de esta función.
c# contiene cadena
Una vez que se agregan todos los nodos a la cola, los nodos agregados en la cola se eliminan llamando a la función de salida de cola que seguirá eliminando un elemento de la cola hasta que se encuentre el nodo nulo del árbol binario. Cada vez que se elimina un nodo del árbol binario de la cola, la variable de profundidad que representa la profundidad del árbol binario se incrementa en uno. Y al final, el valor de la variable de profundidad representará la profundidad final del árbol binario.
