ALGORITMO DE FLOYD WARSHALL

El Algoritmo de Floyd-Warshall , llamado así por sus creadores. Robert Floyd y Stephen Warshall , es un algoritmo fundamental en informática y teoría de grafos. Se utiliza para encontrar los caminos más cortos entre todos los pares de nodos en un gráfico ponderado. Este algoritmo es altamente eficiente y puede manejar gráficos con ambos positivo y N pesos de borde negativos , lo que la convierte en una herramienta versátil para resolver una amplia gama de problemas de red y conectividad.

Tabla de contenidos

Algoritmo de Floyd Warshall
Idea detrás del algoritmo Floyd Warshall
Algoritmo del algoritmo de Floyd Warshall
Pseudocódigo del algoritmo Floyd Warshall
Ilustración del algoritmo de Floyd Warshall
Análisis de complejidad del algoritmo Floyd Warshall
¿Por qué el algoritmo Floyd-Warshall es mejor para gráficos densos y no para gráficos dispersos?
Preguntas importantes de la entrevista relacionadas con Floyd-Warshall
Aplicaciones del mundo real del algoritmo Floyd-Warshall

Banner-algoritmo-de-Floyd-Warshall

Algoritmo de Floyd Warshall:

El Algoritmo de Floyd Warshall es un algoritmo de ruta más corta para todos los pares a diferencia de Dijkstra y Botones Ford que son algoritmos de ruta más corta de fuente única. Este algoritmo funciona tanto para el dirigido y ponderado no dirigido gráficos. Pero no funciona para los gráficos con ciclos negativos (donde la suma de las aristas en un ciclo es negativa). Sigue Programación dinámica enfoque para verificar cada ruta posible que pasa por cada nodo posible para calcular la distancia más corta entre cada par de nodos.
es una relación

Idea detrás del algoritmo Floyd Warshall:

Supongamos que tenemos una gráfica GRAMO[][] con EN vértices de 1 a norte . Ahora tenemos que evaluar una MatrixPathMatrix[][] más corto donde s hortestPathMatrix[i][j] representa el camino más corto entre vértices i y j .

Obviamente el camino más corto entre i a j tendrá algunos k número de nodos intermedios. La idea detrás del algoritmo de floyd warshall es tratar todos y cada uno de los vértices de 1 a norte como nodo intermedio uno por uno.

La siguiente figura muestra la propiedad de subestructura óptima anterior en el algoritmo de Floyd Warshall:

Algoritmo del algoritmo de Floyd Warshall:

Inicialice la matriz de solución igual que la matriz del gráfico de entrada como primer paso.
Luego actualice la matriz solución considerando todos los vértices como un vértice intermedio.
La idea es seleccionar todos los vértices uno por uno y actualizar todos los caminos más cortos que incluyen el vértice seleccionado como vértice intermedio en el camino más corto.
Cuando elegimos el número de vértice k como vértice intermedio, ya hemos considerado vértices {0, 1, 2, .. k-1} como vértices intermedios.
Por cada par (yo, j) de los vértices de origen y destino respectivamente, hay dos casos posibles.
- k no es un vértice intermedio en el camino más corto desde i a j . Mantenemos el valor de dist[i][j] como están las cosas.
- k es un vértice intermedio en el camino más corto desde i a j . Actualizamos el valor de dist[i][j] como dist[i][k] + dist[k][j], si dist[i][j]> dist[i][k] + dist[k][j]

Pseudocódigo del algoritmo Floyd Warshall:`>`

Para k = 0 an – 1
Para i = 0 an – 1
Para j = 0 an – 1
Distancia[i, j] = min(Distancia[i, j], Distancia[i, k] + Distancia[k, j])

donde i = Nodo de origen, j = Nodo de destino, k = Nodo intermedio

Ilustración del algoritmo de Floyd Warshall:

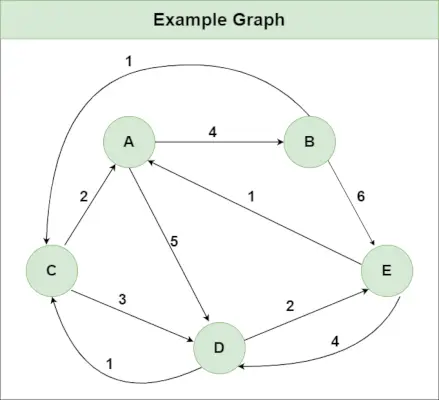
Supongamos que tenemos un gráfico como se muestra en la imagen:
organización y arquitectura de la computadora

Paso 1 : Inicialice la matriz Distancia[][] utilizando el gráfico de entrada de modo que Distancia[i][j]= peso del borde desde i a j , también Distancia[i][j] = Infinito si no hay ningún borde desde i a j.

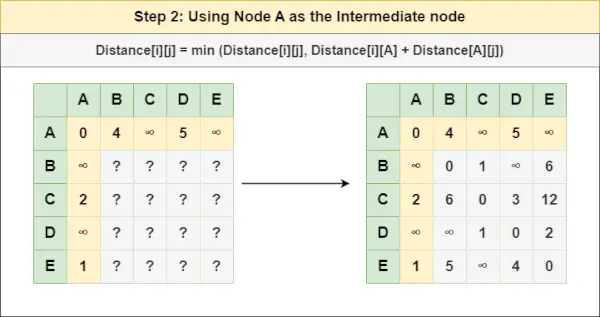
Paso 2 : Tratar el nodo A como nodo intermedio y calcule la Distancia[][] para cada par de nodos {i,j} usando la fórmula:

= Distancia[i][j] = mínimo (Distancia[i][j], (Distancia de i a A ) + (Distancia desde A a j ))
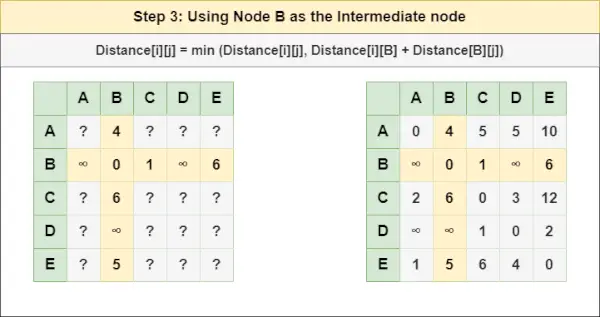
= Distancia[i][j] = mínimo (Distancia[i][j], Distancia[i][ A ] + Distancia[ A ][j])

Paso 3 : Tratar el nodo B como nodo intermedio y calcule la Distancia[][] para cada par de nodos {i,j} usando la fórmula:

= Distancia[i][j] = mínimo (Distancia[i][j], (Distancia de i a B ) + (Distancia desde B a j ))
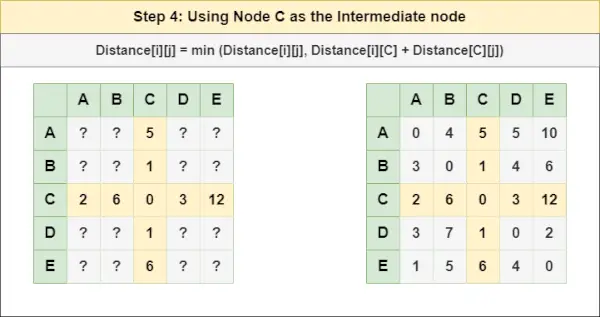
= Distancia[i][j] = mínimo (Distancia[i][j], Distancia[i][ B ] + Distancia[ B ][j])
entrada estándar en c

Etapa 4 : Tratar el nodo C como nodo intermedio y calcule la Distancia[][] para cada par de nodos {i,j} usando la fórmula:

= Distancia[i][j] = mínimo (Distancia[i][j], (Distancia de i a C ) + (Distancia desde C a j ))
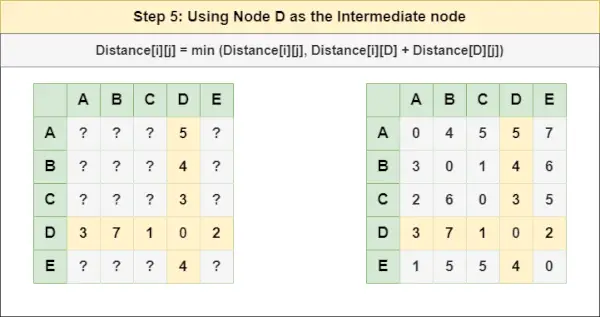
= Distancia[i][j] = mínimo (Distancia[i][j], Distancia[i][ C ] + Distancia[ C ][j])

Paso 5 : Tratar el nodo D como nodo intermedio y calcule la Distancia[][] para cada par de nodos {i,j} usando la fórmula:

= Distancia[i][j] = mínimo (Distancia[i][j], (Distancia de i a D ) + (Distancia desde D a j ))
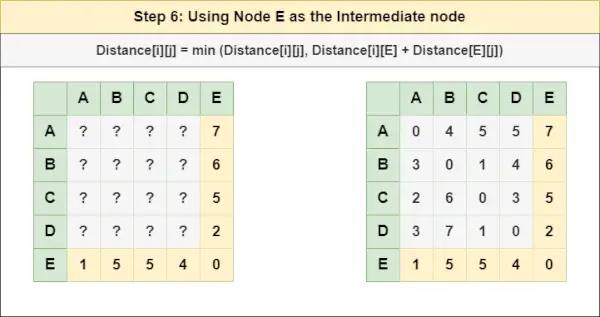
= Distancia[i][j] = mínimo (Distancia[i][j], Distancia[i][ D ] + Distancia[ D ][j])

Paso 6 : Tratar el nodo Y como nodo intermedio y calcule la Distancia[][] para cada par de nodos {i,j} usando la fórmula:

= Distancia[i][j] = mínimo (Distancia[i][j], (Distancia de i a Y ) + (Distancia desde Y a j ))
= Distancia[i][j] = mínimo (Distancia[i][j], Distancia[i][ Y ] + Distancia[ Y ][j])

Paso 7 : Dado que todos los nodos han sido tratados como un nodo intermedio, ahora podemos devolver la matriz Distancia[][] actualizada como nuestra matriz de respuesta.

Práctica recomendada ¡Pruébelo!

A continuación se muestra la implementación del enfoque anterior:

C++

 // C++ Program for Floyd Warshall Algorithm #include  using namespace std; // Number of vertices in the graph #define V 4 /* Define Infinite as a large enough value.This value will be used for vertices not connected to each other */ #define INF 99999 // A function to print the solution matrix void printSolution(int dist[][V]); // Solves the all-pairs shortest path // problem using Floyd Warshall algorithm void floydWarshall(int dist[][V]) {  int i, j, k;  /* Add all vertices one by one to  the set of intermediate vertices.  --->Antes del inicio de una iteración, tenemos distancias más cortas entre todos los pares de vértices, de modo que las distancias más cortas consideran solo los vértices del conjunto {0, 1, 2, .. k-1} como vértices intermedios.  ----> Después del final de una iteración, el vértice no. k se suma al conjunto de vértices intermedios y el conjunto se convierte en {0, 1, 2, .. k} */ para (k = 0; k< V; k++) {  // Pick all vertices as source one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination for the  // above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest path from  // i to j, then update the value of  // dist[i][j]  if (dist[i][j]>(dist[i][k] + dist[k][j]) && (dist[k][j] != INF && dist[i][k] != INF)) dist[i][j] = dist[i][k] + dist[k][j];  } } } // Imprime la matriz de distancia más corta printSolution(dist); } /* Una función de utilidad para imprimir la solución */ void printSolution(int dist[][V]) { cout<< 'The following matrix shows the shortest '  'distances'  ' between every pair of vertices 
';  for (int i = 0; i < V; i++) {  for (int j = 0; j < V; j++) {  if (dist[i][j] == INF)  cout << 'INF'  << ' ';  else  cout << dist[i][j] << ' ';  }  cout << endl;  } } // Driver's code int main() {  /* Let us create the following weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int gráfico[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0 } };  // Llamada a función floydWarshall(graph);  devolver 0; } // Este código es una contribución de Mythri J L>

 // C Program for Floyd Warshall Algorithm #include  // Number of vertices in the graph #define V 4 /* Define Infinite as a large enough  value. This value will be used  for vertices not connected to each other */ #define INF 99999 // A function to print the solution matrix void printSolution(int dist[][V]); // Solves the all-pairs shortest path // problem using Floyd Warshall algorithm void floydWarshall(int dist[][V]) {  int i, j, k;  /* Add all vertices one by one to  the set of intermediate vertices.  --->Antes del inicio de una iteración, tenemos distancias más cortas entre todos los pares de vértices, de modo que las distancias más cortas consideran solo los vértices del conjunto {0, 1, 2, .. k-1} como vértices intermedios.  ----> Después del final de una iteración, el vértice no. k se suma al conjunto de vértices intermedios y el conjunto se convierte en {0, 1, 2, .. k} */ para (k = 0; k< V; k++) {  // Pick all vertices as source one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination for the  // above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest path from  // i to j, then update the value of  // dist[i][j]  if (dist[i][k] + dist[k][j] < dist[i][j])  dist[i][j] = dist[i][k] + dist[k][j];  }  }  }  // Print the shortest distance matrix  printSolution(dist); } /* A utility function to print solution */ void printSolution(int dist[][V]) {  printf(  'The following matrix shows the shortest distances'  ' between every pair of vertices 
');  for (int i = 0; i < V; i++) {  for (int j = 0; j < V; j++) {  if (dist[i][j] == INF)  printf('%7s', 'INF');  else  printf('%7d', dist[i][j]);  }  printf('
');  } } // driver's code int main() {  /* Let us create the following weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int gráfico[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0 } };  // Llamada a función floydWarshall(graph);  devolver 0; }>

Java

 // Java program for Floyd Warshall All Pairs Shortest // Path algorithm. import java.io.*; import java.lang.*; import java.util.*; class AllPairShortestPath {  final static int INF = 99999, V = 4;  void floydWarshall(int dist[][])  {  int i, j, k;  /* Add all vertices one by one  to the set of intermediate  vertices.  --->Antes del inicio de una iteración, tenemos distancias más cortas entre todos los pares de vértices, de modo que las distancias más cortas consideran solo los vértices del conjunto {0, 1, 2, .. k-1} como vértices intermedios.  ----> Después del final de una iteración, el vértice no. k se suma al conjunto de vértices intermedios y el conjunto se convierte en {0, 1, 2, .. k} */ para (k = 0; k< V; k++) {  // Pick all vertices as source one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination for the  // above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest path  // from i to j, then update the value of  // dist[i][j]  if (dist[i][k] + dist[k][j]  < dist[i][j])  dist[i][j]  = dist[i][k] + dist[k][j];  }  }  }  // Print the shortest distance matrix  printSolution(dist);  }  void printSolution(int dist[][])  {  System.out.println(  'The following matrix shows the shortest '  + 'distances between every pair of vertices');  for (int i = 0; i < V; ++i) {  for (int j = 0; j < V; ++j) {  if (dist[i][j] == INF)  System.out.print('INF ');  else  System.out.print(dist[i][j] + ' ');  }  System.out.println();  }  }  // Driver's code  public static void main(String[] args)  {  /* Let us create the following weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int gráfico[][] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0 } };  AllPairShortestPath a = nuevo AllPairShortestPath();  // Llamada a función a.floydWarshall(graph);  } } // Contribuido por Aakash Hasija>

Python3

 # Python3 Program for Floyd Warshall Algorithm # Number of vertices in the graph V = 4 # Define infinity as the large # enough value. This value will be # used for vertices not connected to each other INF = 99999 # Solves all pair shortest path # via Floyd Warshall Algorithm def floydWarshall(graph):  ''' dist[][] will be the output   matrix that will finally  have the shortest distances   between every pair of vertices '''  ''' initializing the solution matrix   same as input graph matrix  OR we can say that the initial   values of shortest distances  are based on shortest paths considering no   intermediate vertices ''' dist = list(map(lambda i: list(map(lambda j: j, i)), graph))  ''' Add all vertices one by one   to the set of intermediate  vertices.  --->Antes del inicio de una iteración, tenemos distancias más cortas entre todos los pares de vértices, de modo que las distancias más cortas consideran solo los vértices del conjunto {0, 1, 2, .. k-1} como vértices intermedios.  ----> Después del final de una iteración, el vértice no. k se agrega al conjunto de vértices intermedios y el conjunto se convierte en {0, 1, 2, .. k} ''' para k en el rango (V): # elige todos los vértices como fuente uno por uno para i en rango(V): # Elija todos los vértices como destino para la # fuente seleccionada arriba para j en rango(V): # Si el vértice k está en la ruta más corta desde # i a j, actualice el valor de dist[i][ j] dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j] ) printSolution(dist) # Una función de utilidad para imprimir la solución def printSolution (dist): print('La siguiente matriz muestra las distancias más cortas entre cada par de vértices') para i en el rango(V): para j en el rango(V): if(dist[i][j] == INF): print('%7s' % ('INF'), end=' ') else: print('%7d	' % (dist[i][j]), end=' ') if j == V-1: print() # Código del conductor if __name__ == '__main__': ''' 10 (0)------ ->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 ''' gráfico = [[0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0 , 1], [INF, INF, INF, 0] ] # Llamada a función floydWarshall(graph) # Este código es una contribución de Mythri J L>

 // C# program for Floyd Warshall All // Pairs Shortest Path algorithm. using System; public class AllPairShortestPath {  readonly static int INF = 99999, V = 4;  void floydWarshall(int[, ] graph)  {  int[, ] dist = new int[V, V];  int i, j, k;  // Initialize the solution matrix  // same as input graph matrix  // Or we can say the initial  // values of shortest distances  // are based on shortest paths  // considering no intermediate  // vertex  for (i = 0; i < V; i++) {  for (j = 0; j < V; j++) {  dist[i, j] = graph[i, j];  }  }  /* Add all vertices one by one to  the set of intermediate vertices.  --->Antes del inicio de una iteración, tenemos distancias más cortas entre todos los pares de vértices, de modo que las distancias más cortas consideran solo los vértices del conjunto {0, 1, 2, .. k-1} como vértices intermedios.  ---> Después del final de una iteración, el vértice no. k se agrega al conjunto de vértices intermedios y el conjunto se convierte en {0, 1, 2, .. k} */ para (k = 0; k< V; k++) {  // Pick all vertices as source  // one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination  // for the above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest  // path from i to j, then update  // the value of dist[i][j]  if (dist[i, k] + dist[k, j]  < dist[i, j]) {  dist[i, j]  = dist[i, k] + dist[k, j];  }  }  }  }  // Print the shortest distance matrix  printSolution(dist);  }  void printSolution(int[, ] dist)  {  Console.WriteLine(  'Following matrix shows the shortest '  + 'distances between every pair of vertices');  for (int i = 0; i < V; ++i) {  for (int j = 0; j < V; ++j) {  if (dist[i, j] == INF) {  Console.Write('INF ');  }  else {  Console.Write(dist[i, j] + ' ');  }  }  Console.WriteLine();  }  }  // Driver's Code  public static void Main(string[] args)  {  /* Let us create the following  weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int[, ] gráfico = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0 , 1 }, { INF, INF, INF, 0 } };  AllPairShortestPath a = nuevo AllPairShortestPath();  // Llamada a función a.floydWarshall(graph);  } } // Este artículo es una contribución de // Abdul Mateen Mohammed>

JavaScript

 // A JavaScript program for Floyd Warshall All  // Pairs Shortest Path algorithm.  var INF = 99999;  class AllPairShortestPath {  constructor() {  this.V = 4;  }  floydWarshall(graph) {  var dist = Array.from(Array(this.V), () =>new Array(this.V).fill(0));  var i, j, k;  // Inicializa la matriz de solución // igual que la matriz del gráfico de entrada // O podemos decir que los // valores iniciales de las distancias más cortas // se basan en los caminos más cortos // sin considerar ningún // vértice intermedio para (i = 0; i< this.V; i++) {  for (j = 0; j < this.V; j++) {  dist[i][j] = graph[i][j];  }  }  /* Add all vertices one by one to  the set of intermediate vertices.  --->Antes del inicio de una iteración, tenemos distancias más cortas entre todos los pares de vértices, de modo que las distancias más cortas consideran solo los vértices del conjunto {0, 1, 2, .. k-1} como vértices intermedios.  ---> Después del final de una iteración, el vértice no. k se suma al conjunto de vértices intermedios y el conjunto se convierte en {0, 1, 2, .. k} */ para (k = 0; k< this.V; k++) {  // Pick all vertices as source  // one by one  for (i = 0; i < this.V; i++) {  // Pick all vertices as destination  // for the above picked source  for (j = 0; j < this.V; j++) {  // If vertex k is on the shortest  // path from i to j, then update  // the value of dist[i][j]  if (dist[i][k] + dist[k][j] < dist[i][j]) {  dist[i][j] = dist[i][k] + dist[k][j];  }  }  }  }  // Print the shortest distance matrix  this.printSolution(dist);  }  printSolution(dist) {  document.write(  'Following matrix shows the shortest ' +  'distances between every pair of vertices '  );  for (var i = 0; i < this.V; ++i) {  for (var j = 0; j < this.V; ++j) {  if (dist[i][j] == INF) {  document.write(' INF ');  } else {  document.write('  ' + dist[i][j] + ' ');  }  }  document.write(' ');  }  }  }  // Driver Code  /* Let us create the following  weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ var gráfico = [ [0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0, 1] , [INF, INF, INF, 0], ];  var a = nuevo AllPairShortestPath();  // Imprime la solución a.floydWarshall(graph);    // Este código es aportado por rdtaank.>

PHP

  // PHP Program for Floyd Warshall Algorithm  // Solves the all-pairs shortest path problem // using Floyd Warshall algorithm  function floydWarshall ($graph, $V, $INF) { /* dist[][] will be the output matrix   that will finally have the shortest   distances between every pair of vertices */ $dist = array(array(0,0,0,0), array(0,0,0,0), array(0,0,0,0), array(0,0,0,0)); /* Initialize the solution matrix same   as input graph matrix. Or we can say the   initial values of shortest distances are   based on shortest paths considering no   intermediate vertex. */ for ($i = 0; $i < $V; $i++) for ($j = 0; $j < $V; $j++) $dist[$i][$j] = $graph[$i][$j]; /* Add all vertices one by one to the set   of intermediate vertices.   --->Antes del inicio de una iteración, tenemos distancias más cortas entre todos los pares de vértices, de modo que las distancias más cortas consideran solo los vértices del conjunto {0, 1, 2, .. k-1} como vértices intermedios.   ----> Después del final de una iteración, el vértice no. k se agrega al conjunto de vértices intermedios y el conjunto se convierte en {0, 1, 2, .. k} */ for ($k = 0; $k< $V; $k++) { // Pick all vertices as source one by one  for ($i = 0; $i < $V; $i++) { // Pick all vertices as destination  // for the above picked source  for ($j = 0; $j < $V; $j++) { // If vertex k is on the shortest path from  // i to j, then update the value of dist[i][j]  if ($dist[$i][$k] + $dist[$k][$j] < $dist[$i][$j]) $dist[$i][$j] = $dist[$i][$k] + $dist[$k][$j]; } } } // Print the shortest distance matrix  printSolution($dist, $V, $INF); } /* A utility function to print solution */ function printSolution($dist, $V, $INF) { echo 'The following matrix shows the ' . 'shortest distances between ' . 'every pair of vertices 
'; for ($i = 0; $i < $V; $i++) { for ($j = 0; $j < $V; $j++) { if ($dist[$i][$j] == $INF) echo 'INF ' ; else echo $dist[$i][$j], ' '; } echo '
'; } } // Drivers' Code // Number of vertices in the graph  $V = 4 ; /* Define Infinite as a large enough  value. This value will be used for vertices not connected to each other */ $INF = 99999 ; /* Let us create the following weighted graph   10  (0)------->(3) | /| 5 | |   | | 1 |/ |  (1)------->(2) 3 */ $gráfico = matriz(matriz(0, 5, $INF, 10), matriz($INF, 0, 3, $INF), matriz($ INF, $INF, 0, 1), matriz($INF, $INF, $INF, 0)); // Llamada a función floydWarshall($graph, $V, $INF); // ¿Este código es aportado por Ryuga?>>

Producción

The following matrix shows the shortest distances between every pair of vertices 0 5 8 9 INF 0 3 4 INF INF 0 1 INF INF INF 0>

Análisis de complejidad del algoritmo Floyd Warshall:

Complejidad del tiempo: O(V³), donde V es el número de vértices en el gráfico y ejecutamos tres bucles anidados cada uno de tamaño V
Espacio Auxiliar: O(V²), para crear una matriz 2-D con el fin de almacenar la distancia más corta para cada par de nodos.

Nota : El programa anterior sólo imprime las distancias más cortas. Podemos modificar la solución para imprimir las rutas más cortas también almacenando la información del predecesor en una matriz 2D separada.

tamaño de fuente de látex

¿Por qué el algoritmo Floyd-Warshall es mejor para gráficos densos y no para gráficos dispersos?

Gráfico denso : Un gráfico en el que el número de aristas es significativamente mayor que el número de vértices.
Gráfico disperso : Un gráfico en el que el número de aristas es muy bajo.

No importa cuántas aristas haya en el gráfico, Algoritmo de Floyd Warshall corre para O(V³) veces por lo que es más adecuado para Gráficos densos . En el caso de gráficos dispersos, Algoritmo de Johnson es más adecuado.

¿Cómo detectar un ciclo negativo en un gráfico utilizando el algoritmo Floyd Warshall?
¿En qué se diferencia el algoritmo de Floyd-warshall del algoritmo de Dijkstra?
¿En qué se diferencia el algoritmo Floyd-warshall del algoritmo Bellman-Ford?

Aplicaciones del mundo real del algoritmo Floyd-Warshall:

En redes de computadoras, el algoritmo se puede utilizar para encontrar el camino más corto entre todos los pares de nodos en una red. Esto se denomina como enrutamiento de red .
Conectividad de vuelo En la industria de la aviación para encontrar el camino más corto entre los aeropuertos.
SIG ( Sistemas de Información Geográfica ) las aplicaciones a menudo implican el análisis de datos espaciales, como redes de carreteras, para encontrar los caminos más cortos entre ubicaciones.
El algoritmo de Kleene que es una generalización de floyd warshall, se puede utilizar para encontrar expresiones regulares para un lenguaje regular.