El árbol de expresiones es un árbol que se utiliza para representar las distintas expresiones. La estructura de datos de árbol se utiliza para representar las declaraciones expresivas. En este árbol, el nodo interno siempre indica los operadores.
- Los nodos hoja siempre indican los operandos.
- Las operaciones siempre se realizan sobre estos operandos.
- El operador presente en la profundidad del árbol siempre tiene la máxima prioridad.
- El operador que se encuentra poco en la profundidad del árbol siempre tiene la prioridad más baja en comparación con los operadores que se encuentran en la profundidad.
- El operando siempre estará presente en una profundidad del árbol; de ahí que se considere el más alta prioridad entre todos los operadores.
- En resumen, podemos resumirlo como el valor presente en la profundidad del árbol tiene la máxima prioridad en comparación con los otros operadores presentes en la parte superior del árbol.
- El uso principal de estos árboles de expresión es que se utiliza para evaluar, analizar y modificar las diversas expresiones.
- También se utiliza para conocer la asociatividad de cada operador en la expresión.
- Por ejemplo, el operador + es asociativo por izquierda y / es asociativo por derecha.
- El dilema de esta asociatividad se ha solucionado utilizando la expresión árboles.
- Estos árboles de expresión se forman mediante el uso de una gramática libre de contexto.
- Hemos asociado una regla en gramáticas libres de contexto delante de cada producción gramatical.
- Estas reglas también se conocen como reglas semánticas y, al utilizarlas, podemos construir fácilmente árboles de expresión.
- Es una de las partes principales del diseño del compilador y pertenece a la fase de análisis semántico.
- En este análisis semántico, utilizaremos las traducciones dirigidas por la sintaxis y, como resultado, generaremos el árbol de análisis anotado.
- Un árbol de análisis anotado no es más que el análisis simple asociado con el atributo de tipo y cada regla de producción.
- El objetivo principal del uso de árboles de expresión es crear expresiones complejas y pueden evaluarse fácilmente utilizando estos árboles de expresión.
- Es inmutable y una vez que hemos creado un árbol de expresión, no podemos cambiarlo ni modificarlo más.
- Para realizar más modificaciones, es necesario construir el nuevo árbol de expresión por completo.
- También se utiliza para resolver la evaluación de expresiones de sufijo, prefijo e infijo.
Los árboles de expresión juegan un papel muy importante en la representación de nivel de idioma código en forma de datos, que se almacena principalmente en una estructura en forma de árbol. También se utiliza en la representación en memoria del lambda expresión. Usando la estructura de datos de árbol, podemos expresar la expresión lambda de manera más transparente y explícita. Primero se crea para convertir el segmento de código en el segmento de datos para que la expresión pueda evaluarse fácilmente.
El árbol de expresión es un árbol binario en el que cada nodo externo u hoja corresponde al operando y cada nodo interno o padre corresponde a los operadores, por ejemplo el árbol de expresión para 7 + ((1+8)*3) sería:
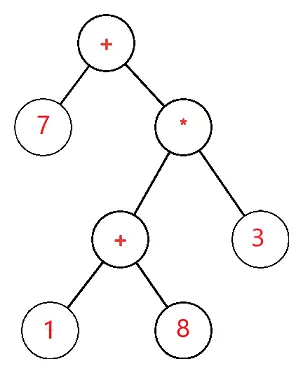
Sea S el árbol de expresión
Si S no es nulo, entonces
Si S.value es un operando, entonces
Devolver valor S
x = resolver(S.izquierda)
y = resolver(S.derecha)
Calcular de retorno (x, y, valor S.)
Aquí, en el ejemplo anterior, el árbol de expresiones utilizó gramática libre de contexto.
Tenemos algunas producciones asociadas a algunas reglas de producción en esta gramática, conocidas principalmente como reglas semánticas . Podemos definir la producción de resultados a partir de las reglas de producción correspondientes utilizando estas reglas semánticas. Aquí hemos utilizado el parámetro de valor, que calculará el resultado y lo devolverá al símbolo de inicio de la gramática. S.left calculará el hijo izquierdo del nodo y, de manera similar, el hijo derecho del nodo se puede calcular utilizando el parámetro S.right.
Uso del árbol de expresión
- El objetivo principal del uso de árboles de expresión es crear expresiones complejas y pueden evaluarse fácilmente utilizando estos árboles de expresión.
- También se utiliza para conocer la asociatividad de cada operador en la expresión.
- También se utiliza para resolver la evaluación de expresiones de sufijo, prefijo e infijo.
Implementación de un árbol de expresión.
Para implementar el árbol de expresión y escribir su programa, se nos pedirá que utilicemos una estructura de datos de pila.
Como sabemos que la pila se basa en el principio LIFO de último en entrar, primero en salir, el elemento de datos insertado recientemente en la pila se ha extraído cuando sea necesario. Para su implementación se utilizan las dos operaciones principales de la pila, push y pop. Usando la operación push, insertaremos el elemento de datos en la pila y, usando la operación pop, eliminaremos el elemento de datos de la pila.
Funciones principales de la pila en la implementación del árbol de expresión:
En primer lugar, escanearemos la expresión dada de izquierda a derecha, luego, uno por uno, verificaremos el carácter identificado.
- Si un carácter escaneado es un operando, aplicaremos la operación de inserción y lo insertaremos en la pila.
- Si un carácter escaneado es un operador, le aplicaremos la operación pop para eliminar los dos valores de la pila y convertirlos en su hijo, y luego devolveremos el nodo principal actual a la pila.
Implementación del árbol de expresión en lenguaje de programación C.
// C program for expression tree implementation #include #include /* The below structure node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ struct node { char info ; struct node* l ; struct node* r ; struct node* nxt ; }; struct node *head=NULL; /* Helper function that allocates a new node with the given data and NULL left and right pointers. */ struct node* newnode(char data) { struct node* node = (struct node*) malloc ( sizeof ( struct node ) ) ; node->info = data ; node->l = NULL ; node->r = NULL ; node->nxt = NULL ; return ( node ) ; } void Inorder(struct node* node) { if ( node == NULL) return ; else { /* first recur on left child */ Inorder ( node->l ) ; /* then print the data of node */ printf ( '%c ' , node->info ) ; /* now recur on right child */ Inorder ( node->r ) ; } } void push ( struct node* x ) { if ( head == NULL ) head = x ; else { ( x )->nxt = head ; head = x ; } // struct node* temp ; // while ( temp != NULL ) // { // printf ( ' %c ' , temp->info ) ; // temp = temp->nxt ; // } } struct node* pop() { // Poping out the top most [pointed with head] element struct node* n = head ; head = head->nxt ; return n ; } int main() { char t[] = { 'X' , 'Y' , 'Z' , '*' , '+' , 'W' , '/' } ; int n = sizeof(t) / sizeof(t[0]) ; int i ; struct node *p , *q , *s ; for ( i = 0 ; i <n ; i++ ) { if read character is operator then popping two other elements from stack and making a binary tree ( t[i]="=" '+' || '-' '*' ' '^' s="newnode" t [ i ] p="pop()" q="pop()" s->l = q ; s->r = p; push(s); } else { s = newnode ( t [ i ] ) ; push ( s ) ; } } printf ( ' The Inorder Traversal of Expression Tree: ' ) ; Inorder ( s ) ; return 0 ; } </n> El resultado del programa anterior es:
X + Y * Z / W
Implementación del árbol de expresión en lenguaje de programación C++.
// C++ program for expression tree #include using namespace std ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class node { public: char info ; node* l ; node* r ; node* nxt = NULL ; node ( char c ) { this->info = c ; l = NULL ; r = NULL ; } node() { l = NULL ; r = NULL ; } friend class Stack ; friend class tree ; } ; class Stack { node* head = NULL ; public: void push ( node* ) ; node* pop() ; friend class tree ; } ; class tree { public: void inorder ( node* x ) { // cout<<'tree in inorder traversal is: '<l ) ; cout <info <r } void stack::push( node* x { if ( head="=" null we are inserting here nodes at the top of stack [following lifo principle] else x->nxt = head ; head = x ; } } node* Stack::pop() { // Poping out the top most [ pointed with head ] element node* p = head ; head = head->nxt ; return p ; } int main() { string str = 'XYZ*+W/' ; // If you wish take input from user: //cout << 'Insert Postorder Expression: ' <> s; Stack s ; tree t ; node *p, *q, *re; int n = str.length() ; for ( int i = 0 ; i <n ; i++ ) { if ( str[ i ]="=" '+' || '-' '*' ' '^') re="new" node( str[i] p="s.pop()" q="s.pop()" re->l = q ; re->r = p ; s.push(re) ; } else { re = new node( str[ i ] ) ; s.push(re) ; } } cout << ' The Inorder Traversal of Expression Tree: ' ; t.inorder(re) ; return 0 ; } </n></'tree> El resultado del programa anterior es:
X + Y * Z / W
Implementación del árbol de expresión en el lenguaje de programación Java.
// Java program for expression tree import java.util.* ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class Node { char info ; Node l , r ; public Node(char data) { this.info = data ; l = null ; r = null ; } } public class Main { public static boolean isOperator ( char ch ) { if ( ch == '+' || ch == '-' || ch == '*' || ch == '/' || ch == '^' ) { return true ; } return false ; } public static Node Tree ( String postfix ) { Stack st = new Stack(); Node t1,t2,temp ; for ( int i = 0 ; i <p> <strong>The output of the above program is:</strong> </p> <pre> X + Y * Z / W </pre> <hr> 