Una NFA puede tener cero, uno o más de un movimiento desde un estado determinado en un símbolo de entrada determinado. Una NFA también puede tener movimientos NULL (movimientos sin símbolo de entrada). Por otro lado, DFA tiene un solo movimiento desde un estado determinado en un símbolo de entrada determinado.
Pasos para convertir NFA a DFA:
Paso 1: convertir el NFA dado a su tabla de transición equivalente
Para convertir la NFA a su tabla de transición equivalente, necesitamos enumerar todos los estados, símbolos de entrada y reglas de transición. Las reglas de transición se representan en forma de matriz, donde las filas representan el estado actual, las columnas representan el símbolo de entrada y las celdas representan el siguiente estado.
Paso 2: crear el estado inicial de DFA
El estado inicial del DFA es el conjunto de todos los estados iniciales posibles en el NFA. Este conjunto se denomina cierre épsilon del estado inicial de la NFA. El cierre épsilon es el conjunto de todos los estados que se pueden alcanzar desde el estado inicial siguiendo transiciones épsilon (?).
Paso 3: crear la tabla de transición de DFA
La tabla de transición de la DFA es similar a la tabla de transición de la NFA, pero en lugar de estados individuales, las filas y columnas representan conjuntos de estados. Para cada símbolo de entrada, la celda correspondiente en la tabla de transición contiene el cierre épsilon del conjunto de estados obtenidos siguiendo las reglas de transición en la tabla de transición de la NFA.
Paso 4: crear los estados finales del DFA
Los estados finales de la DFA son los conjuntos de estados que contienen al menos un estado final de la NFA.
Paso 5: Simplifique el DFA
El DFA obtenido en los pasos anteriores puede contener estados y transiciones innecesarios. Para simplificar el DFA, podemos utilizar las siguientes técnicas:
- Eliminar estados inalcanzables: los estados a los que no se puede llegar desde el estado inicial se pueden eliminar de DFA.
- Eliminar estados muertos: los estados que no pueden conducir a un estado final pueden eliminarse del DFA.
- Fusionar estados equivalentes: los estados que tienen las mismas reglas de transición para todos los símbolos de entrada se pueden fusionar en un solo estado.
Paso 6: Repita los pasos 3 a 5 hasta que no sea posible realizar más simplificaciones.
Después de simplificar el DFA, repetimos los pasos 3 a 5 hasta que no sea posible realizar más simplificaciones. El DFA final obtenido es el DFA minimizado equivalente al NFA dado.
Ejemplo: Considere la siguiente NFA que se muestra en la Figura 1.

A continuación se detallan los diversos parámetros para NFA. Q = { q0, q1, q2 } ? = ( a, b ) F = { q2 } ? (Función de transición de NFA)
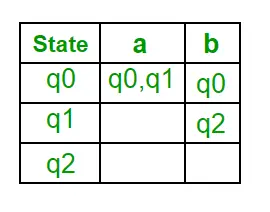
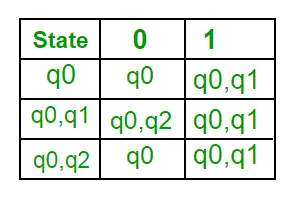
Paso 1: Q’ = ? Paso 2: Q’ = {q0} Paso 3: Para cada estado en Q’, encuentre los estados para cada símbolo de entrada. Actualmente, el estado en Q' es q0, encuentre movimientos desde q0 en los símbolos de entrada a y b usando la función de transición de NFA y actualice la tabla de transición de DFA. ?’ (Función de transición de DFA)

Ahora {q0, q1} se considerará como un solo estado. Como su entrada no está en Q’, agréguela a Q’. Entonces Q' = { q0, { q0, q1 } } Ahora, los movimientos desde el estado { q0, q1 } en diferentes símbolos de entrada no están presentes en la tabla de transición de DFA, lo calcularemos como: ?' , a ) = ? (q0,a)? ? ( q1, a ) = { q0, q1 } ?’ ( { q0, q1 }, b ) = ? (q0,b)? ? ( q1, b ) = { q0, q2 } Ahora actualizaremos la tabla de transición de DFA. ?’ (Función de transición de DFA)

Ahora {q0, q2} se considerará como un solo estado. Como su entrada no está en Q’, agréguela a Q’. Entonces Q' = { q0, { q0, q1 }, { q0, q2 } } Ahora, los movimientos desde el estado {q0, q2} en diferentes símbolos de entrada no están presentes en la tabla de transición de DFA, lo calcularemos como: ?' ( { q0, q2 }, a ) = ? (q0,a)? ? ( q2, a ) = { q0, q1 } ?’ ( { q0, q2 }, b ) = ? (q0,b)? ? ( q2, b ) = { q0 } Ahora actualizaremos la tabla de transición de DFA. ?’ (Función de transición de DFA)
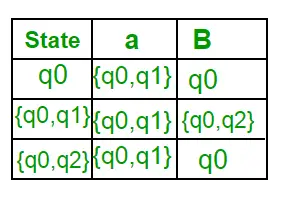
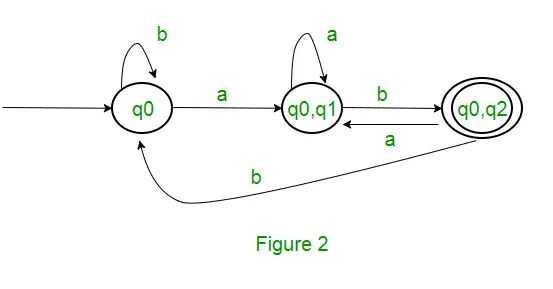
Como no se genera ningún nuevo estado, hemos terminado con la conversión. El estado final de DFA será el estado que tiene q2 como componente, es decir, {q0, q2} A continuación se muestran los diversos parámetros de DFA. Q’ = { q0, { q0, q1 }, { q0, q2 } } ? = ( a, b ) F = { { q0, q2 } } y función de transición?’ como se muestra arriba. El DFA final para el NFA anterior se muestra en la Figura 2.
Nota : A veces, no es fácil convertir expresiones regulares a DFA. Primero puede convertir expresiones regulares a NFA y luego de NFA a DFA.
Pregunta : El número de estados en el autómata finito determinista mínimo correspondiente a la expresión regular (0 + 1)* (10) es ____________.
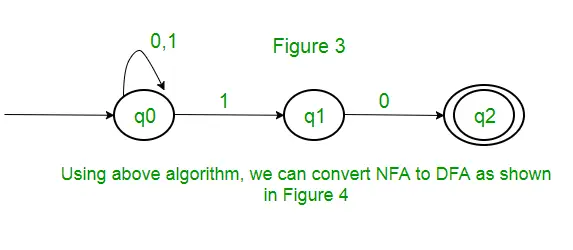
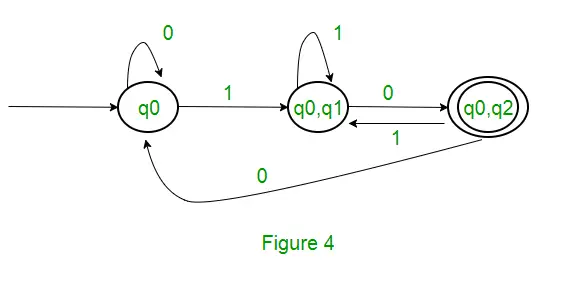
Solución : Primero, haremos un NFA para la expresión anterior. Para hacer un NFA para (0 + 1)*, NFA estará en el mismo estado q0 en el símbolo de entrada 0 o 1. Luego, para la concatenación, agregaremos dos movimientos (q0 a q1 para 1 y q1 a q2 para 0) como se muestra en la Figura 3.
Este artículo ha sido contribuido por Sonal Tuteja.
