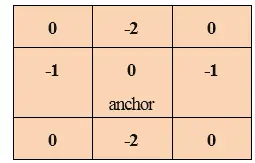
La convolución se usa para muchas cosas como calcular derivadas, detectar bordes, aplicar desenfoques, etc. y todo esto se hace usando un 'núcleo de convolución'. Un núcleo de convolución es una matriz muy pequeña y en esta matriz, cada celda tiene un número y también un punto de anclaje.
El punto de anclaje se utiliza para conocer la posición del kernel con respecto a la imagen. Comienza en la esquina superior izquierda de la imagen y se mueve en cada píxel de forma secuencial. El kernel superpone algunos píxeles en cada posición de la imagen. Cada píxel que se superpone se multiplica y luego se suma. Y la suma se establece como el valor de la posición actual.
opacidad de transición css
La convolución es el proceso en el que cada elemento de la imagen se agrega a sus vecinos locales y luego el núcleo lo pondera. Está relacionado con una forma de convolución matemática.
En Convolución, la matriz no realiza la multiplicación de matrices tradicional, pero se denota con *.
Supongamos que hay dos matrices de 3x3, una es el núcleo y la otra es una pieza de imagen. En la convolución, las filas y columnas del núcleo se invierten, luego se multiplican y luego se realiza la suma. Los elementos que están presentes en el centro de la matriz, es decir, en [2,2] de la imagen, serán una combinación ponderada de la matriz de la imagen y los pesos los dará el núcleo. De manera similar, se ponderarán todos los demás elementos de la matriz y luego se calcularán las ponderaciones.
A continuación se muestra un pseudocódigo para describir el proceso de convolución:
¿Qué hace Ravel en Python?
For each image row in input image: For each pixel in image row: Set accumulator to zero For each kernel row in kernel: For each element in kernel row: If element position corresponding* to pixel position then Multiply element value corresponding*to pixelvalue Add result to accumulator Endif Set output image pixel to accumulator
La convolución se puede calcular utilizando múltiples bucles for. Pero el uso de bucles for provoca muchos cálculos repetidos y también aumenta el tamaño de la imagen y el núcleo. Utilizando la técnica de Transformada Discreta de Fourier, el cálculo de la convolución se puede realizar rápidamente. En esta técnica, toda la operación de convolución se convierte en una simple multiplicación.
En convolución, el problema ocurre cuando el núcleo está cerca del borde o de las esquinas porque el núcleo es bidimensional.
Para superar estos problemas se pueden hacer las siguientes cosas:
- Unos pueden ser ignorados
- Se pueden crear píxeles adicionales cerca de los bordes.
Se pueden crear píxeles adicionales de las siguientes maneras:
- Píxel de borde duplicado.
- Reflejar bordes
- Los píxeles se pueden copiar desde el otro extremo.
